
【题目】在平面直角坐标系xOy中,已知直线l:x﹣y﹣2=0,抛物线C:y2=2px(p>0),若抛物线C上存在关于直线l对称的相异两点P和Q.
(1)求证:线段PQ的中点坐标为(2﹣p,﹣p);
(2)求p的取值范围.
【答案】
(1)解:∵抛物线C上存在关于直线l对称的相异两点P和Q,
∴直线l是线段PQ的垂直平分线∴PQ的斜率为﹣1,
设PQ的方程为:y=﹣x+b,P(x1,y1),Q(x2,y2),
线段PQ的中点为M(xM,yM),由 ![]() ,
,
∴x2﹣2(p+b)x+b2=0(*),
∴ ![]() ,
,
∴x1+x2=2(p+b),
∴xM=(p+b),∴M(p+b,﹣p),
又∵M在直线l上,∴p+b﹣(﹣p)﹣2=0,
∴b=2﹣2p,
∴线段PQ的中点坐标为(2﹣p,﹣p)
(2)解:在(1)中(*)式:x2﹣2(p+b)x+b2=0及b=2﹣2p,
∴x2﹣2(2﹣p)x+(2﹣2p)2=0
∵相交于P、Q两点
∴△=(4﹣2p)2﹣4(2﹣2p)2>0
∴3p2﹣4p<0,∴ ![]() .
.
【解析】(1)根据题意得到:直线l是线段PQ的垂直平分线,从而设出直线PQ的方程,将问题转化为:直线PQ与抛物线C交于点P,Q,求线段PQ的中点M的坐标;(2)将相交于P,Q两点变为医院二次方程有两个实数根来求得p的取值范围.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数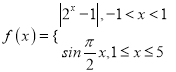 ,有如下结论
,有如下结论
①函数f(x)的值域是[-1,1];
②函数f(x)的减区间为[1,3];
③若存在实数x1、x2、x3、x4,满足x1<x2<x3<x4,且f(x1)=f(x2)=f(x3)=f(x4),则x1+x2<0;
④在③的条件下x3+x4=6;
⑤若方程f(x)=a有3个解,则![]() <a≤1
<a≤1
其中正确的是
A. ①②③ B. ③④⑤ C. ②③⑤ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义“等和数列”:在一个数列中,如果每一个项与它的后一项的和都为同一个常数,那么这个数列就叫做“等和数列”,这个常数叫做公和.已知数列{an}是等和数列,且a1=2,公和为6,求这个数列的前n项的和S= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆M过点P(10,4),且与直线4x+3y-20=0相切于点A(2,4)
(1)求圆M的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且![]() ,求直线l的方程;
,求直线l的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某班50人进行智力测验,其得分如下:
48,64,52,86,71,48,64,41,86,79,71,68,82,84,68,64,62,68,81,57,90,52,74,73,56,78,47,66,55,64,56,88,69,40,73,97,68,56,67,59,70,52,79,44,55,69,62,58,32,58.
(1)这次测试成绩的最大值和最小值各是多少?
(2)将[30,100)平分成7个小区间,试画出该班学生智力测验成绩的频数分布图.
(3)分析这个频数分布图,你能得出什么结论?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com