
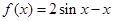 ,
, .
.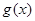 在
在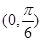 内和在
内和在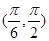 内的零点情况.
内的零点情况.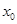 是
是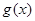 在
在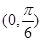 内的一个零点,求
内的一个零点,求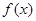 在
在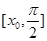 上的最值.
上的最值.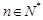 恒有
恒有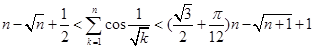 .
. 在
在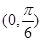 内有唯一零点;
内有唯一零点; 在
在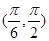 内无零点.(2)
内无零点.(2) 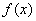 在
在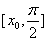 有最大值
有最大值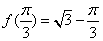 ;
;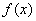 在
在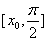 的最小值
的最小值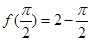 .(3)详见解析.
.(3)详见解析. 在
在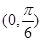 、
、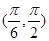 内的单调性,然后根据零点判定定理确定
内的单调性,然后根据零点判定定理确定 的零点情况; (2)求导得
的零点情况; (2)求导得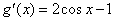 ,所以
,所以  在
在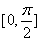 有最大值
有最大值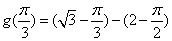 ,又
,又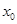 是
是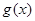 在
在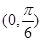 内的一个零点,所以
内的一个零点,所以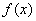 在
在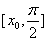 的最大值为
的最大值为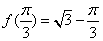 .再由(1)的结论知
.再由(1)的结论知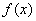 在
在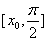 的最小值应为
的最小值应为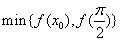 .由
.由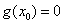 知
知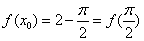 ,于是
,于是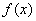 在
在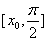 的最小值
的最小值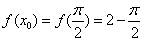 . (3)由(2)知
. (3)由(2)知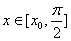 时,有
时,有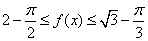 ,即
,即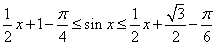 ,得
,得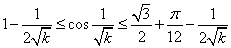 ,再将左右两边放缩相加即得.
,再将左右两边放缩相加即得.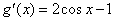 在
在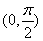 有唯一零点
有唯一零点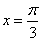 ,易知
,易知 在
在 单增而在
单增而在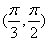
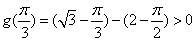 ,故
,故 在
在 和
和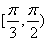 内都至多有一个零点.
内都至多有一个零点.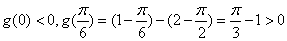 ,
, 在
在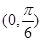 内有唯一零点;
内有唯一零点;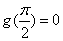 知
知 在
在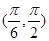 内无零点.
内无零点. 在
在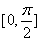 有最大值
有最大值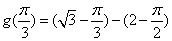 ,
,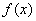 在
在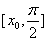 有最大值
有最大值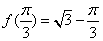 ;
;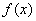 在
在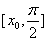 的最小值应为
的最小值应为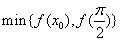 .
.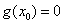 知
知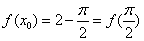 ,于是
,于是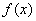 在
在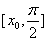 的最小值
的最小值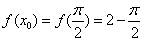 .
.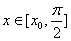 时,有
时,有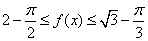 ,即
,即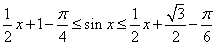 ①
①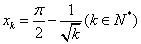 ,则
,则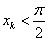 且
且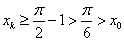 ,将
,将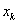 的值代入①中,可得
的值代入①中,可得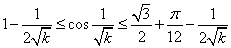
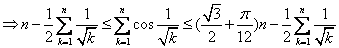 ②
②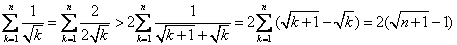 ,得
,得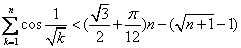 ③
③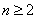 时,
时,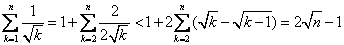 ,故
,故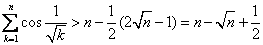 ④
④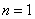 时④即
时④即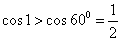 ,显然也成立.故原不等式成立.
,显然也成立.故原不等式成立.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
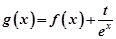 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;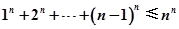 (n∈N*).
(n∈N*).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
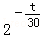 ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )| A.5太贝克 | B.75In2太贝克 | C.150In2太贝克 | D.150太贝克 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com