
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的极值大于
的极值大于![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间
,单调递减区间
为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间. (2)存在,范围为
,无单调递减区间. (2)存在,范围为![]()
【解析】
试题(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
① 当![]() 时,
时,![]() ,∵
,∵![]() ∴
∴![]() ,∴ 函数
,∴ 函数![]() 单调递增区间为
单调递增区间为![]()
② 当![]() 时,令
时,令![]() 得
得![]() ,即
,即![]() ,
,![]() .
.
(ⅰ)当![]() ,即
,即![]() 时,得
时,得![]() ,故
,故![]() ,
,
∴ 函数![]() 的单调递增区间为
的单调递增区间为![]() .
.
(ⅱ)当![]() ,即
,即![]() 时,方程
时,方程![]() 的两个实根分别为
的两个实根分别为![]() ,
,![]() .
.
若![]() ,则
,则![]() ,此时,当
,此时,当![]() 时,
时,![]() .
.
∴函数![]() 的单调递增区间为
的单调递增区间为![]() ,若
,若![]() ,则
,则![]() ,此时,当
,此时,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
∴函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间
,单调递减区间
为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
(2)由(1)得当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,故函数
上单调递增,故函数![]() 无极值
无极值
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,
,
∴![]() 有极大值,其值为
有极大值,其值为![]() ,其中
,其中![]() .
.
∵![]() ,即
,即![]() , ∴
, ∴![]() .
.
设函数![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上为增函数,又
上为增函数,又![]() ,则
,则![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]()
![]() .
.
即![]() ,结合
,结合![]() 解得
解得![]() ,∴实数
,∴实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】春节期间,由于高速公路继续实行小型车免费,因此高速公路上车辆较多,某调查公司在某城市从七座以下小型汽车中按进入服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图的频率分布直方图.
(Ⅰ)此调查公司在采样中,用到的是什么抽样方法?
(Ⅱ)求这40辆小型车辆车速的众数、中位数以及平均数的估计值;
(Ⅲ)若从车速在[60,70)的车辆中任抽取2辆,求至少有一辆车的车速在[65,70)的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照![]() 分成5组,制成如图所示频率分直方图.
分成5组,制成如图所示频率分直方图.

(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在![]() 内的男生数与女生数3:2,若在满意度评分值为
内的男生数与女生数3:2,若在满意度评分值为![]() 的人中随机抽取2人进行座谈,求2人均为男生的概率.
的人中随机抽取2人进行座谈,求2人均为男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高中男生中随机选取100名学生,将他们的体重(单位: ![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.

(1)估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);
(2)若要从体重在![]() ,
, ![]() 内的两组男生中,用分层抽样的方法选取5人,再从这5人中随机抽取3人,记体重在
内的两组男生中,用分层抽样的方法选取5人,再从这5人中随机抽取3人,记体重在![]() 内的人数为
内的人数为![]() ,求其分布列和数学期望
,求其分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两点M(4,﹣2),N(2,4).
(1)求MN的垂直平分线方程;
(2)直线l经过点A(3,0),且点M和点N到直线l的距离相等,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点![]() ,
,![]() 两点,且圆心C在直线
两点,且圆心C在直线![]() 上.
上.
(1)求圆C的方程;
(2)设![]() ,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使
,对圆C上任意一点P,在直线MC上是否存在与点M不重合的点N,使![]() 是常数,若存在,求出点N坐标;若不存在,说明理由.
是常数,若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是y=f(x)导函数的图象,对于下列四个判断:
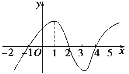
①f(x)在[-2,-1]上是增函数;
②x=-1是f(x)的极小值点;
③f(x)在[-1,2]上是增函数,在[2,4]上是减函数;
④x=3是f(x)的极小值点.
其中判断正确的是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com