
分析 实数x,y满足logax+2logxa+logxy=-3,化为logax+$\frac{2}{lo{g}_{a}x}$+$\frac{lo{g}_{a}y}{lo{g}_{a}x}$=-3,令logax=t,化为:logay=$-(t+\frac{3}{2})^{2}$+$\frac{1}{4}$,再利用二次函数的单调性、对数的运算性质即可得出.
解答 解:实数x,y满足logax+2logxa+logxy=-3,
化为logax+$\frac{2}{lo{g}_{a}x}$+$\frac{lo{g}_{a}y}{lo{g}_{a}x}$=-3,
令logax=t,
化为:logay=$-(t+\frac{3}{2})^{2}$+$\frac{1}{4}$,
∵a>1,∴当t=-$\frac{3}{2}$时,y取得最大值$\sqrt{2}$,
∴$lo{g}_{a}\sqrt{2}$=$\frac{1}{4}$,
解得a=4.
∴log4x=-$\frac{3}{2}$,
∴x=${4}^{-\frac{3}{2}}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查了二次函数的单调性、对数的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | 20 | B. | 5$\sqrt{2}$ | C. | 4($\sqrt{5}$+1) | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.
如图,抛物线C1:x2=2py(p>0)与椭圆C2:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个交点为T($\frac{4}{3}$,$\frac{1}{3}$),F(1,0)为椭圆C2的右焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
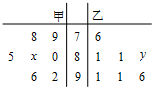 某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )
某中学高三文科班从甲、乙两个班各选出7名学生参加文史知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则x+y的值为( )| A. | 8 | B. | 7 | C. | 9 | D. | 168 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
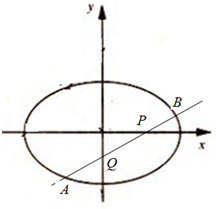 已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1,过点P(1,0)作直线l,使l交椭圆于A,B两点,且交y轴于Q点,若|AQ|=|BP|.求直线l的方程.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| M | 900 | 700 | 300 | 100 |
| y | 0.5 | 3.5 | 6.5 | 9.5 |
| M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com