
分析 逐个判断:向量是可自由平移的,命题①、②均不正确;举反例,可证③不正确,由空间向量基本定理,可知,命题④不正确.
解答 解:由于向量是可自由平移的,所以向量 $\overrightarrow a$、$\overrightarrow b$共线,不一定向量$\overrightarrow a$、$\overrightarrow b$所在的直线平行,故命题①不正确;
同样因为向量是可自由平移的,向量 $\overrightarrow a$、$\overrightarrow b$所在的直线为异面直线,则向量 $\overrightarrow a$、$\overrightarrow b$也可能共面,故命题②不正确;
三个向量 $\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$两两共面,如直角坐标系的三个基向量,它们不共面,故命题③不正确;
由空间向量基本定理,可知,只有当三个向量 $\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$,不共面的时候,由它们做基底,才有后面的结论,故命题④不正确.
即4个命题都不正确.
故答案是:0.
点评 本题为判断命题的真假,涉及向量共线与空间向量基本定理,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=x3+x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2或$\frac{1}{2}$ | B. | 2或-$\frac{1}{2}$ | C. | 2或$\frac{1}{2}$ | D. | -2或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单位向量都相等 | |
| B. | 长度相等且方向相反的两个向量不一定是共线向量 | |
| C. | 若$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|$>$|{\overrightarrow b}|$且$\overrightarrow a$与$\overrightarrow b$同向,则$\overrightarrow a$>$\overrightarrow b$ | |
| D. | 对于任意向量$\overrightarrow a$,$\overrightarrow b$,必有$|{\overrightarrow a+\overrightarrow b}|$≤$|{\overrightarrow a}|$+$|{\overrightarrow b}|$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
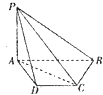 如图所示,四棱锥P-ABCD的底面为等腰梯形,AB∥DC,AB=2AD,若PA⊥平面ABCD,∠ABC=60°
如图所示,四棱锥P-ABCD的底面为等腰梯形,AB∥DC,AB=2AD,若PA⊥平面ABCD,∠ABC=60°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2sin5 | B. | -2cos5 | C. | 2sin5 | D. | 2cos5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com