
���� ��1������a1=S1��an=Sn-Sn-1����n��1�����ɵ�an�������¶��弴���жϣ�
��2�����õȲ����е�ͨ�ʽ�����ʽ���ɵ�m�������¶��弴�����d=-1��
��3����dn=bn��b�dz����������ǰn��ͣ���bn=na1��cn=��d-a1����n-1���������¶���ɵ���an=bn+cn�����ɵ�֤��
��� �⣺��1����Sn=3n��n��N*������a1=S1��an=Sn-Sn-1����n��1����
�ɵ�an=$\left\{\begin{array}{l}{3��n=1}\\{2•{3}^{n-1}��n��2}\end{array}\right.$����n=2ʱ��9=2•3n-1����m∉N*�����Բ��ǡ�E���С���
��2��������{bn}�ǵȲ����У�������b1=1������d��0��
�ɵ�n+$\frac{n��n-1��}{2}$d=1+��m-1��d����Ϊm=$\frac{n-1}{d}$+$\frac{n��n-1��}{2}$+1��
$\frac{n��n-1��}{2}$Ϊ�Ǹ���������������$\frac{n-1}{d}$Ҫ��Ϊ������dΪ���зǸ������Ĺ�Լ����d��0��
����d=-1��
��3��֤�������ȣ���dn=bn��b�dz�������
������{dn}ǰn���ΪSn=$\frac{n��n-1��}{2}$b������{dn}�еĵ�$\frac{n��n-1��}{2}$�
���{dn}�ǡ�E���С���
������ĵȲ�����{an}��an=a1+��n-1��d��dΪ�����
��bn=na1��cn=��d-a1����n-1����
��an=bn+cn��
������{bn}��{cn}���ǡ�E���С���
�ʶ�����ĵȲ�����{an}���ܴ���������E���С�{bn}��{cn}��
ʹ��an=bn+cn��n��N*��������
���� ���⿼���¶������������ã�����Ȳ����е�ͨ�����ͣ��������������������������е��⣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017����Ϻ������и�����ѧ���¿�����ѧ�������Ծ��������棩 ���ͣ�ѡ����
��֪����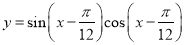 ���������ж���ȷ���ǣ� ��
���������ж���ȷ���ǣ� ��
A���˺�������С������Ϊ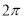 ����ͼ���һ���Գ�������
����ͼ���һ���Գ�������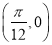
B���˺�������С������Ϊ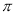 ����ͼ���һ���Գ�������
����ͼ���һ���Գ�������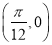
C���˺�������С������Ϊ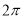 ����ͼ���һ���Գ�������
����ͼ���һ���Գ�������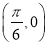
D���˺�������С������Ϊ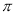 ����ͼ���һ���Գ�������
����ͼ���һ���Գ�������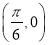
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
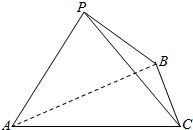 ��ͼ������P-ABC�ĵ����DZ߳�Ϊ2�ĵȱ������Σ���$PA=PB=\sqrt{2}$�������P-BA-C�Ĵ�СΪ60�㣬������P-ABC���������������$\frac{52}{9}��$��
��ͼ������P-ABC�ĵ����DZ߳�Ϊ2�ĵȱ������Σ���$PA=PB=\sqrt{2}$�������P-BA-C�Ĵ�СΪ60�㣬������P-ABC���������������$\frac{52}{9}��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com