
分析 (1)由韦达定理可得 tanα+tanβ 和tanαtanβ,利用两角和的正切公式求出tan(α+β)的值,由α+β 的范围求出α+β 的值.
(2)由α+β 的值,可求2(α+β)的值,利用正切函数的图象可求tan2(α+β)的值.
解答 解:(1)由韦达定理可得 tanα+tanβ=5,tanαtanβ=6,
故有 tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=-1,
又tanα>0,tanβ>0,且α,β∈(0,π),
∴α,β∈(0,$\frac{π}{2}$),α+β∈(0,π),
∴α+β=$\frac{3π}{4}$.
(2)∵α+β=$\frac{3π}{4}$.
∴2(α+β)=$\frac{3π}{2}$,
∴tan2(α+β)的值不存在.
点评 本题考查两角和的正切公式,正切函数的图象,根据三角函数的值求角,求出α+β=$\frac{3π}{4}$,是解题的关键,属于基础题.


科目:高中数学 来源: 题型:选择题
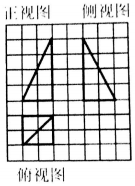 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体外接球的表面积为( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体外接球的表面积为( )| A. | 8π | B. | 16π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
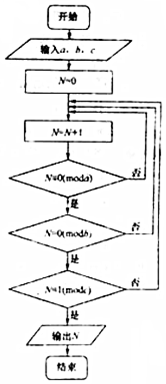 若正整数N除以正整m后的余数为n,则记为N=n(modm),例如10=4(mod6).如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )
若正整数N除以正整m后的余数为n,则记为N=n(modm),例如10=4(mod6).如图程序框图的算法源于我国古代《孙子算经》中的“孙子定律”的某一环节,执行该框图,输入a=2,b=3,c=5,则输出的N=( )| A. | 6 | B. | 9 | C. | 12 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | (1,+∞) | C. | (-∞,0) | D. | (-∞,$\frac{1}{e}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com