
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
分析 以A为原点,以BC的垂直平分线为y轴,建立直角坐标系.由于等边三角形△的边长为4,可得B,C的坐标,再利用向量的坐标运算和数乘运算可得$\overrightarrow{AD}$,$\overrightarrow{AP}$,利用△APD的面积公式即可得出.
解答 解:以A为原点,以BC的垂直平分线为y轴,建立直角坐标系.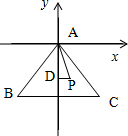
∵等边三角形△的边长为4,
∴B(-2,-2$\sqrt{3}$),C(2,-2$\sqrt{3}$),
由足$\overrightarrow{AD}=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})$=$\frac{1}{4}$[(-2,-2$\sqrt{3}$)+(2,-2$\sqrt{3}$)]=(0,-$\sqrt{3}$),
$\overrightarrow{AP}=\overrightarrow{AD}+\frac{1}{8}\overrightarrow{BC}$=(0,-$\sqrt{3}$)+$\frac{1}{8}$(4,0)=($\frac{1}{2}$,-$\sqrt{3}$),
∴△ADP的面积为S=$\frac{1}{2}$|$\overrightarrow{AD}$|•|$\overrightarrow{DP}$|=$\frac{1}{2}$×$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{4}$,
故选:A.
点评 本题考查了向量的坐标运算和数乘运算、三角形的面积计算公式,属于中档题.


科目:高中数学 来源: 题型:选择题
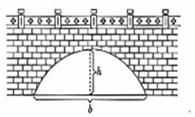
| A. | h2 | B. | 2h2 | C. | $\frac{3}{2}$h2 | D. | $\frac{7}{4}$h2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=cos({2x+\frac{π}{2}})$ | B. | y=sin22x-cos22x | C. | y=sin2x+cos2x | D. | y=sin2xcos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com