
 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| | 满意 | 一般 | 不满意 |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
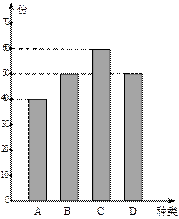
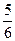
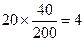 份.
份. =“同学甲被选中进行问卷调查”, 则
=“同学甲被选中进行问卷调查”, 则 .
.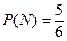 .
.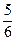 .
.

 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
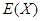 及方差
及方差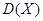 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
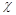 2≥6.635, 而P(
2≥6.635, 而P(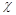 2≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系。
2≥6.635)≈0.01,则有99% 的把握认为两个分类变量有关系。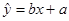 过点
过点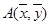 。
。 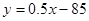 中,变量x=200时,变量y的值一定是15。
中,变量x=200时,变量y的值一定是15。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
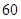 名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1))网购金额超过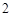 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过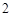 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为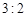 .
.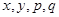 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).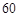 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定 人,若需从这
人,若需从这 人中随机选取
人中随机选取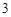 人进行问卷调查,设
人进行问卷调查,设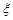 为选取的
为选取的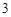 人中“网购红人”的人数,求
人中“网购红人”的人数,求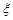 的分布列和数学期望.
的分布列和数学期望.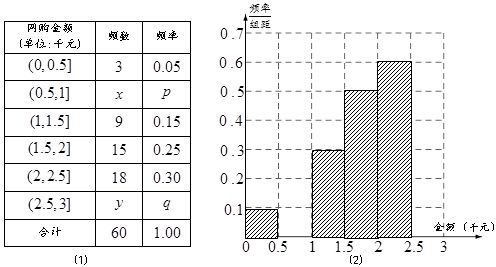
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [150,160) | [160,165) | [165,170) | [170,175) | [175,180] |
| 频数 | 2 | 12 | 16 | 6 | 3 | 1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y有关” |
| B.在犯错误的概率不超过0.1%的前提下,认为“变量X与变量Y无关” |
| C.有99%以上的把握认为“变量X与变量Y无关” |
| D.有99%以上的把握认为“变量X与变量Y有关” |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 100 | 150 | 150 | 50 |
| 抽取人数 | | 6 | | | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com