
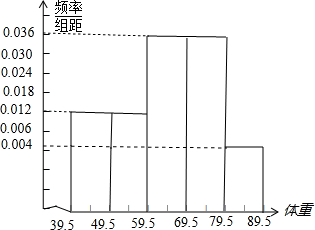
 某校为了解学生的体重发育情况,现从600名高一男生体检评价报告单中随机抽出50名学生的体重(单位:kg)数据进行整理后分成五组,得到频率分布表如下:
某校为了解学生的体重发育情况,现从600名高一男生体检评价报告单中随机抽出50名学生的体重(单位:kg)数据进行整理后分成五组,得到频率分布表如下:| 分组 | 频数 | 频率 | |
| 一 | 39.5-49.5 | 6 | 0.12 |
| 二 | 49.5-59.5 | a | 0.12 |
| 三 | 59.5-69.5 | 18 | c |
| 四 | 69.5-79.5 | b | d |
| 五 | 79.5-89.5 | 2 | 0.04 |
| 合计 | 50 | e | |
| 600 |
| 50 |
| 24 |
| 50 |


科目:高中数学 来源: 题型:
| f(x) |
| x |
| 1-x |
| 1+x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| AB |
| e1 |
| e2 |
| BC |
| e1 |
| e2 |
| CD |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com