
分析 (1)设P(x,y),由点到直线的距离公式和两点的距离公式,可得,$\frac{{\sqrt{{{(x+1)}^2}+{y^2}}}}{|x+4|}=\frac{1}{2}$,化简即可得到所求轨迹方程;
(2)设A(x1,y1),B(x2,y2),运用两点的距离公式和斜率公式,结合点A、B在椭圆C上,可得x12+x22=4,
讨论①当x1=x2时,则四边形ABA1B1为矩形;②当x1≠x2时,通过三角形的面积公式和椭圆的对称性,即可得到所求面积为定值.
解答 解:(1)设P(x,y),由题意可得,$\frac{{\sqrt{{{(x+1)}^2}+{y^2}}}}{|x+4|}=\frac{1}{2}$,
化简得3x2+4y2=12,
所以,动点P的轨迹C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)设A(x1,y1),B(x2,y2),
由${k_{OA}}•{k_{OB}}=-\frac{3}{4}$,得$\frac{{{y_1}{y_2}}}{{{x_1}{x_2}}}=-\frac{3}{4}$,
$|AB|=\sqrt{{{({x_1}-{x_2})}^2}+{{({y_1}-{y_2})}^2}}$,
因为点A、B在椭圆C上,
所以$y_1^2=3({1-\frac{x_1^2}{4}})$,$y_2^2=3({1-\frac{x_2^2}{4}})$,
所以,$9x_1^2x_2^2=16y_1^2y_2^2$=$9(4-x_1^2)(4-x_2^2)$,
化简得$x_1^2+x_2^2=4$.
①当x1=x2时,则四边形ABA1B1为矩形,y2=-y1,则$\frac{y_1^2}{x_1^2}=\frac{3}{4}$,
由$y_1^2=3({1-\frac{x_1^2}{4}})$,得$\frac{3}{4}x_1^2=3({1-\frac{x_1^2}{4}})$,
解得$x_1^2=2$,$y_1^2=\frac{3}{2}$,S=|AB|•|A1B|=4|x1||y1|=$4\sqrt{3}$;
②当x1≠x2时,直线AB的方向向量为$\vec d=({x_2}-{x_1}\;,\;{y_2}-{y_1})$,
直线AB的方程为(y2-y1)x-(x2-x1)y+x2y1-x1y2=0,
原点O到直线AB的距离为$d=\frac{{|{x_1}{y_2}-{x_2}{y_1}|}}{{\sqrt{{{({x_2}-{x_1})}^2}+{{({y_2}-{y_1})}^2}}}}$,
所以△AOB的面积${S_{△AOB}}=\frac{1}{2}•|AB|•d=\frac{1}{2}|{x_1}{y_2}-{x_2}{y_1}|$,
根据椭圆的对称性,四边形ABA1B1的面积S=4S△AOB=2|x1y2-x2y1|,
所以,${S^2}=4{({x_1}{y_2}-{x_2}{y_1})^2}=4(x_1^2y_2^2-2{x_1}{x_2}{y_1}{y_2}+x_2^2y_1^2)$
=$4[{3x_1^2({1-\frac{x_2^2}{4}})+\frac{3}{2}x_1^2x_2^2+3x_2^2({1-\frac{x_1^2}{4}})}]=12(x_1^2+x_2^2)=48$,
所以$S=4\sqrt{3}$.
所以,四边形ABA1B1的面积为定值$4\sqrt{3}$.
点评 本题考查轨迹方程的求法,注意运用点到直线的距离公式,考查直线的斜率公式和两点的距离公式的运用,考查化简整理的运算能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,$\frac{29}{4}$) | B. | (21,$\frac{135}{4}$) | C. | [27,30) | D. | (27,$\frac{135}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
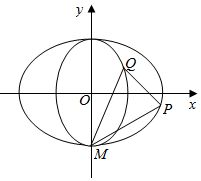 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点M(0,-$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点M(0,-$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -2+$\sqrt{3}$ | C. | -2-$\sqrt{3}$ | D. | 2±$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)=sinxcosx的最小正周期为π | |
| B. | 函数$f(x)=lnx+\frac{1}{2}x-2$在区间(2,3)内有零点 | |
| C. | 已知函数$f(x)={log_a}({x^2}-2x+2)$,若$f(\frac{1}{2})>0$,则0<a<1 | |
| D. | 在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com