
| A. | ex≥x+1 | B. | ln(x+2)-ln(x+1)$<\frac{1}{x+1}$ | ||
| C. | $\frac{2}{π}$x+cosx≥1+sinx | D. | cosx≥1-$\frac{1}{2}$x2 |
分析 对选项加以判断,运用函数的导数,判断符号可得单调性,对于不恒成立可通过举特殊值,即可得到C不恒成立.
解答 解:对于A,由ex-x-1的导数为ex-1,当x≥0时,导数大于等于0,可得ex-x-1≥0,故A恒成立;
对于B,ln(x+2)-ln(x+1)-$\frac{1}{x+1}$=ln$\frac{x+2}{x+1}$-$\frac{1}{x+1}$=ln(1+$\frac{1}{x+1}$)-$\frac{1}{x+1}$,令t=$\frac{1}{x+1}$(0<t≤1),
ln(1+t)-t的导数为$\frac{1}{1+t}$-1=$\frac{-t}{1+t}$<0,可得ln(1+t)-t<0,即为ln(1+$\frac{1}{x+1}$)<$\frac{1}{x+1}$,故B恒成立;
对于C,取x=$\frac{π}{2}$时,$\frac{2}{π}$•$\frac{π}{2}$+cos$\frac{π}{2}$-1-sin$\frac{π}{2}$=-1<0,故C不恒成立;
对于D,cosx-1+$\frac{1}{2}$x2的导数为-sinx+x,当x≥0时,sinx≤x,可得cosx-1+$\frac{1}{2}$x2≥0,故D恒成立.
综上可得,C不恒成立.
故选:C.
点评 本题考查不等式恒成立问题的解法,注意运用函数的单调性,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:
今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:| 年龄(岁) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] |
| 频数 | m | n | 14 | 12 | 8 | 6 |
| 知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
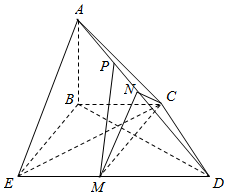 如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,AB=3.M,N分别为DE,AD的中点.
如图所示,平面ABC⊥平面BCDE,BC∥DE,$BC=\frac{1}{2}DE=2$,BE=CD=2,AB⊥BC,AB=3.M,N分别为DE,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组编号 | 年龄分组 | 球迷 | 所占比例 |
| 1 | [20,25) | 1000 | 0.5 |
| 2 | [25,30) | 1800 | 0.6 |
| 3 | [30,35) | 1200 | 0.5 |
| 4 | [35,40) | a | 0.4 |
| 5 | [40,45) | 300 | 0.2 |
| 6 | [45,50] | 200 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com