
【题目】已知函数![]() (e为自然对数的底数),其中
(e为自然对数的底数),其中![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 的两个极值点为
的两个极值点为![]() ,证明:
,证明: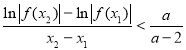 .
.
【答案】(1)答案见解析;(2)证明见解析.
【解析】
(1)先求出![]() ,再对
,再对![]() 分类讨论即得函数的单调性;
分类讨论即得函数的单调性;
(2)求出![]() ,
,![]()
![]() ,转化成证明
,转化成证明![]()
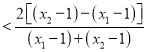 成立,设
成立,设![]() ,
,![]() ,则
,则![]() ,转化成证明
,转化成证明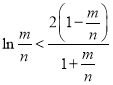 成立,设
成立,设![]() ,则
,则![]() ,构造函数
,构造函数![]() ,
,![]() ,证明
,证明![]() ,即
,即![]() 成立,原题得证.
成立,原题得证.
解:(1)![]() 的定义域
的定义域![]() ,
,![]() ,
,![]() ,
,
方程![]() ,判别式
,判别式![]() ,
,
当![]() 时,
时,![]() ,
,![]() 恒成立,
恒成立,
所以![]()
![]() 恒成立,函数
恒成立,函数![]() 在
在![]() 和
和![]() 上单调递增.
上单调递增.
当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() .
.
所以当![]() 或
或![]() 或
或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 和
和![]() 和
和![]() 是增函数,在
是增函数,在![]() 是减函数.
是减函数.
综上所述:当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和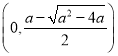 和
和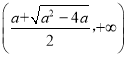 单调递增,在
单调递增,在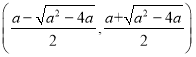 单调递减.
单调递减.
(2)由(1)可知,当![]() 时函数
时函数![]() 存在两个极值点
存在两个极值点![]() ,且
,且![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,且
,且![]() .
.
![]() ,
,![]() ,
,
所以![]()
![]() ,
,
![]()
![]() ,
,
所以![]() ,
,
又![]()
![]()
![]() ,
,
所以,要证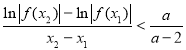 成立,
成立,
即证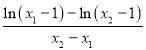
![]() 成立,
成立,
因为且![]() ,所以
,所以
即证![]()
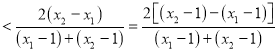 成立,
成立,
设![]() ,
,![]() ,则
,则![]() ,
,
只要证![]() 成立,
成立,
即证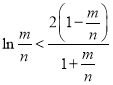 成立.
成立.
设![]() ,则
,则![]() ,构造函数
,构造函数![]() ,
,![]()
则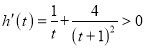 ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,即
,即![]() 成立,
成立,
从而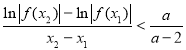 成立.
成立.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】![]() 年,某省将实施新高考,
年,某省将实施新高考,![]() 年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用
年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各
模式,其中语文、数学、外语三科为必考科目,满分各![]() 分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每科目满分
),每科目满分![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取n名学生进行调查.
人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含女生![]() 人,求n的值及抽取到的男生人数;
人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的![]() 列联表,请将下面的列联表补充完整,并判断是否有
列联表,请将下面的列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
(3)在抽取到的![]() 名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出
名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出![]() 名女生,了解女生对“历史”的选课意向情况,在这
名女生,了解女生对“历史”的选课意向情况,在这![]() 名女生中再抽取
名女生中再抽取![]() 人,求这
人,求这![]() 人中选择“历史”的人数为
人中选择“历史”的人数为![]() 人的概率.
人的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: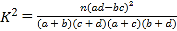 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC的中点.将△ABD沿BD折起,使AB⊥AC,连接AE,AC,DE,得到三棱锥A-BCD.
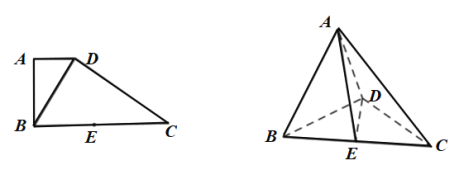
(1)求证:平面ABD⊥平面BCD
(2)若AD=1,二面角C-AB-D的余弦值为![]() ,求二面角B-AD-E的正弦值.
,求二面角B-AD-E的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,且取相等的单位长度,建立平面直角坐标系,直线
轴的正半轴,且取相等的单位长度,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是 (
(![]() 是参数),设点
是参数),设点![]() .
.
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程,将直线
的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且椭圆上一点
,且椭圆上一点![]() 的坐标为
的坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
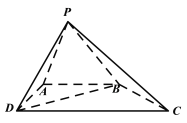
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 在
在![]() 轴正半轴及
轴正半轴及![]() 轴正半轴截距相等时的直角坐标方程;
轴正半轴截距相等时的直角坐标方程;
(2)若![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,点
,点![]() ,求
,求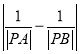 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com