
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据向量的几何意义,向量的数乘运算,三点共线的充要条件便可判断①②叙述正确,再根据向量减法的几何意义即可由③的条件得到$\overrightarrow{CP}={λ}_{1}\overrightarrow{CA}+{λ}_{2}\overrightarrow{CB}$,而根据条件知0<λ1+λ2<1,并且存在k>1,使得kλ1+kλ2=1,并且kλ1,kλ2∈(0,1),$k\overrightarrow{CP}=k{λ}_{1}\overrightarrow{CA}+k{λ}_{2}\overrightarrow{CB}$,这样便可得出点P在△ABC内,从而判断叙述③正确,这样即可得出正确的选项.
解答 解:①λ1=1,λ2=λ3=0时,$\overrightarrow{OP}=\overrightarrow{OA}$$+0\overrightarrow{OB}+0\overrightarrow{OC}$=$\overrightarrow{OA}$;
∴点P和A重合,该叙述正确;
②λ1+λ2=1,λ3=0时,$\overrightarrow{OP}={λ}_{1}\overrightarrow{OA}+{λ}_{2}\overrightarrow{OB}$;
∴P,A,B三点共线;
即点P在直线AB上,该叙述正确;
③λ1+λ2+λ3=1时,λ3=1-λ1-λ2;
∴$\overrightarrow{OP}={λ}_{1}\overrightarrow{OA}+{λ}_{2}\overrightarrow{OB}+(1-{λ}_{1}-{λ}_{2})$$\overrightarrow{OC}$
=${λ}_{1}(\overrightarrow{OA}-\overrightarrow{OC})+{λ}_{2}(\overrightarrow{OB}-\overrightarrow{OC})+\overrightarrow{OC}$
=${λ}_{1}\overrightarrow{CA}+{λ}_{2}\overrightarrow{CB}+\overrightarrow{OC}$;
∴$\overrightarrow{CP}={λ}_{1}\overrightarrow{CA}+{λ}_{2}\overrightarrow{CB}$;
∵0<λ1+λ2<1;
∴存在k>1,使k(λ1+λ2)=1;
如图,设$\overrightarrow{CD}=k\overrightarrow{CP}=k{λ}_{1}\overrightarrow{CA}+k{λ}_{2}\overrightarrow{CB}$: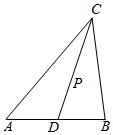
∵kλ1+kλ2=1,且kλ1,kλ2∈(0,1);
∴D在边AB上,不包括A,B点;
∴P在线段CD上,且不包括C,D两点;
∴点P在△ABC内,即该叙述正确;
∴叙述正确个数为3.
故选D.
点评 考查向量、向量加法、减法及向量数乘的几何意义,以及向量的数乘运算,三点A,B,C共线的充要条件:$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,且x+y=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2+$\sqrt{2}$,8] | B. | [2+$\sqrt{2}$,+∞) | C. | [2,+∞) | D. | [2+$\sqrt{2}$,4$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84 | B. | 252 | C. | 761 | D. | 2284 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com