Question

12．在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形，现有如图所示两种方案，则（　　）

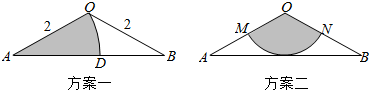
• A． 方案一中扇形的周长更长
• B． 方案二中扇形的周长更长
• C． 方案一中扇形的面积更大
• D． 方案二中扇形的面积更大

Answer 1

分析 由已知利用弧长公式，扇形面积公式求出值比较大小即可．

解答 解：∵△AOB为顶角为120°、腰长为2的等腰三角形，
∴A=B=30°=$\frac{π}{6}$，AM=AN=1，AD=2，
∴方案一中扇形的周长=2$+2+2×\frac{π}{6}$=4+$\frac{π}{3}$，方案二中扇形的周长=1+1+1×$\frac{2π}{3}$=2+$\frac{2π}{3}$，
方案一中扇形的面积=$\frac{1}{2}×2×$2×$\frac{π}{6}$=$\frac{π}{3}$，方案二中扇形的周长=$\frac{1}{2}×\frac{2π}{3}×{1}^{2}$=$\frac{π}{3}$，
故选：A．

点评 本题主要考查了弧长公式，扇形面积公式的应用，考查了计算能力，属于基础题．