
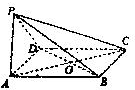
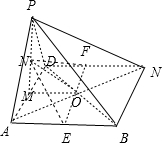
 过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,
过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,| MN2+MO2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
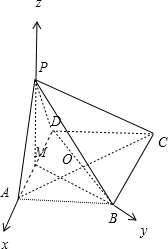 以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,
以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,| 3 |
| 3 |
| 3 |
| PA |
| 3 |
| PB |
| 3 |
| 3 |
| PC |
| 3 |
| 3 |
| n |
|
| 3 |
| n |
| 3 |
| 3 |
| m |
|
| m |
| n |
| m |
|
| ||||
|
|
4
| ||||
|
2
| ||
| 13 |


科目:高中数学 来源: 题型:
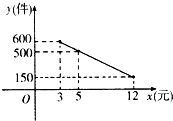 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
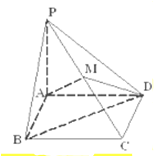 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、-5 | B、-4 | C、-1 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
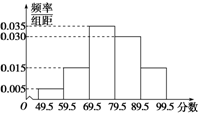 某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )
某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )| A、18篇 | B、24篇 |
| C、25篇 | D、27篇 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com