
| A. | “若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b” | |
| B. | “若(a+b)c=ac+bc”类推出“(a•b)c=ac•bc” | |
| C. | “(ab)n=anbn”类推出“(a+b)n=an+bn” | |
| D. | “若(a+b)c=ac+bc”类推出“$\frac{a+b}{c}$=$\frac{a}{c}$+$\frac{b}{c}$ (c≠0)” |
分析 判断一个推理过程是否是类比推理关键是看他是否符合类比推理的定义,即是否是由特殊到与它类似的另一个特殊的推理过程.另外还要看这个推理过程是否符合实数的性质.
解答 解:对于A:“若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b”是错误的,因为0乘任何数都等于0,
对于B:“若(a+b)c=ac+bc”类推出“(a•b)c=ac•bc”,类推的结果不符合乘法的运算性质,故错误,
对于C:“(ab)n=anbn”类推出“(a+b)n=an+bn”是错误的,如(1+1)2=12+12
对于D:将乘法类推除法,即由“(a+b)c=ac+bc”类推出“$\frac{a+b}{c}$=$\frac{a}{c}$+$\frac{b}{c}$ (c≠0)”是正确的,
故选D.
点评 归纳推理与类比推理不一定正确,我们在进行类比推理时,一定要注意对结论进行进一步的论证,如果要证明一个结论是正确的,要经过严密的论证,但要证明一个结论是错误的,只需要举出一个反例.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:解答题
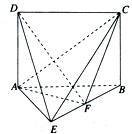 已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,AB=2,AD=$\sqrt{3}$,△ABE为等边三角形,平面ABCD⊥平面ABE,点F为棱BE的中点,
已知几何体E-ABCD如图所示,其中四边形ABCD为矩形,AB=2,AD=$\sqrt{3}$,△ABE为等边三角形,平面ABCD⊥平面ABE,点F为棱BE的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,E是PD的中点.
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,E是PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>$\frac{2\sqrt{3}}{3}$或m<-$\frac{2\sqrt{3}}{3}$ | B. | m<-$\frac{2\sqrt{3}}{3}$或m>0 | C. | m>$\frac{2\sqrt{3}}{3}$ | D. | m<-$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com