
分析 设$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,由题意可得∠C=45°,∠A=60°,由正弦定理可得|$\overrightarrow{a}$|.
解答  解:设$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,
解:设$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,
由题意可得∠C=180°-135°=45°,
∠A=180°-120°=60°,
由正弦定理可得,$\frac{a}{sinA}$=$\frac{c}{sinC}$,
即有a=$\frac{csinA}{sinC}$=$\frac{sin60°}{sin45°}$=$\frac{\sqrt{6}}{2}$,
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查向量的夹角的定义,以及正弦定理的运用,考查运算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(n)中共有n项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$ | |
| B. | f(n)中共有n+1项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | |
| C. | f(n)中共有n2-n项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$ | |
| D. | f(n)中共有n2-n+1项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
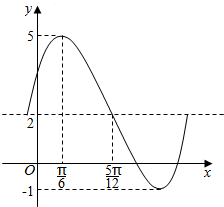 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车次 | 芜湖发车 | 到达马鞍山东 | 耗时 |
| G7174 | 13:37 | 14:02 | 25分钟 |
| G7178 | 15:05 | 15:24 | 19分钟 |
| D5606 | 15:37 | 16:02 | 25分钟 |
| D5608 | 17:29 | 17:48 | 19分钟 |
| G7088 | 18:29 | 18:48 | 19分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
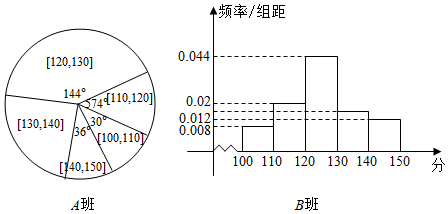
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com