
分析 (I)f(x)=|x|-|2x-1|=$\left\{\begin{array}{l}{x-1,x≤0}\\{3x-1,0<x<\frac{1}{2}}\\{-x+1,x≥\frac{1}{2}}\end{array}\right.$,由f(x,由f(x)>-1,可得:$\left\{\begin{array}{l}{x≤0}\\{x-1>-1}\end{array}\right.$或$\left\{\begin{array}{l}{0<x<\frac{1}{2}}\\{3x-1>-1}\end{array}\right.$或$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{-x+1>-1}\end{array}\right.$,解出即可得出.
(Ⅱ)由(Ⅰ)知:0<a<2,可得:a2-a+1-$\frac{1}{a}$=$\frac{(a-1)({a}^{2}+1)}{a}$=g(a).对a分类讨论:当0<a<1时,当a=1时,当1<a<2时,即可得出.
解答 解:(I)f(x)=|x|-|2x-1|=$\left\{\begin{array}{l}{x-1,x≤0}\\{3x-1,0<x<\frac{1}{2}}\\{-x+1,x≥\frac{1}{2}}\end{array}\right.$,由f(x)>-1,可得:$\left\{\begin{array}{l}{x≤0}\\{x-1>-1}\end{array}\right.$或$\left\{\begin{array}{l}{0<x<\frac{1}{2}}\\{3x-1>-1}\end{array}\right.$或$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{-x+1>-1}\end{array}\right.$,
解得0<x<2,∴M=(0,2).
(Ⅱ)由(Ⅰ)知:0<a<2,∵a2-a+1-$\frac{1}{a}$=$\frac{(a-1)({a}^{2}+1)}{a}$=g(a).
当0<a<1时,g(a)<0,∴a2-a+1<$\frac{1}{a}$;
当a=1时,g(a)=0,∴a2-a+1=$\frac{1}{a}$;
当1<a<2时,g(a)>0,∴a2-a+1>$\frac{1}{a}$;
综上所述:当0<a<1时,∴a2-a+1<$\frac{1}{a}$;
当a=1时,a2-a+1=$\frac{1}{a}$;
当1<a<2时,a2-a+1>$\frac{1}{a}$.
点评 本题考查了不等式的解法、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
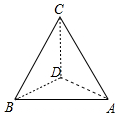 如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$ m.
如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$ m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
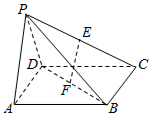 如图,四棱锥P-ABCD的底面是矩形,△PAD为等边三角形,且平面PAD⊥平面ABCD,E,F分别为PC和BD的中点.
如图,四棱锥P-ABCD的底面是矩形,△PAD为等边三角形,且平面PAD⊥平面ABCD,E,F分别为PC和BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com