
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 根据向量数量积的定义求出向量长度和向量夹角进行求解即可.
解答 解:∵$\overrightarrow{BC}$=2$\overrightarrow{BD}$,
∴$\overrightarrow{AD}$•$\overrightarrow{AB}$=($\overrightarrow{AB}$+$\overrightarrow{BD}$)•$\overrightarrow{AB}$=($\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$)•$\overrightarrow{AB}$=$\overrightarrow{AB}$2+$\frac{1}{2}$$\overrightarrow{BC}$•$\overrightarrow{AB}$
=1+$\frac{1}{2}$×1×1cos120°=1-$\frac{1}{2}×\frac{1}{2}$=$\frac{3}{4}$,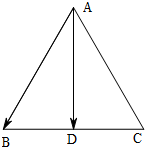
法2.∵$\overrightarrow{BC}$=2$\overrightarrow{BD}$,
∴D是BC的中点,
则在正三角形中,AD=$\frac{\sqrt{3}}{2}$,<$\overrightarrow{AD}$,$\overrightarrow{AB}$>=∠BAD=30°,
则$\overrightarrow{AD}$•$\overrightarrow{AB}$=|$\overrightarrow{AD}$|•|$\overrightarrow{AB}$|cos30°=$\frac{\sqrt{3}}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{3}{4}$
故选:C.
点评 本题主要考查向量数量积的计算,根据向量数量积的定义求出夹角和长度是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∉(0,+∞),lnx≤x-1 | B. | ¬p:?x∈(0,+∞),lnx≤x-1 | ||
| C. | ¬p:?x∉(0,+∞),lnx≥x-1 | D. | ¬p:?x∈(0,+∞),lnx≤x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | [1,2) | C. | [0,2) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b>c+d⇒a>c且b>d | B. | ac2>bc2⇒a>b | ||
| C. | $\frac{c}{a}$>$\frac{b}{d}$⇒ab<cd | D. | $\sqrt{a}$>$\sqrt{b}$?a>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com