
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式和等比数列的中项的性质和等比数列的通项公式,解方程即可得到所求;
(2)求出dn=$\frac{2}{{a}_{n}{a}_{n+1}}$=$\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,运用裂项相消求和,化简即可得到所求和;
(3)求得cn=an•bn=(2n-1)•3n,运用错位相减法求和,结合等比数列的求和公式,化简即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,
a2+a3+a4=15,可得3a1+6d=15,①
a2,a3+4,a4+20为等比数列{bn}的前三项,
可得(a3+4)2=a2(a4+20),
检验(a1+2d+4)2=(a1+d)(a1+3d+20),②
由①②解得a1=1,d=2,
可得an=2n-1,
等比数列{bn}的前三项为3,9,27,
可得公比为3,
即有bn=3n;
(2)数列dn=$\frac{2}{{a}_{n}{a}_{n+1}}$=$\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n+1}$,
的前n项和为Tn=1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$=1-$\frac{1}{2n+1}$=$\frac{2n}{2n+1}$;
(3)cn=an•bn=(2n-1)•3n,
可得前n项和Sn=1•3+3•32+…+(2n-1)•3n,
3Sn=1•32+3•33+…+(2n-1)•3n+1,
两式相减可得,-2Sn=3+2(32+…+3n)-(2n-1)•3n+1
=3+2•$\frac{9(1-{3}^{n-1})}{1-3}$-(2n-1)•3n+1,
化简可得Sn=3+(n-1)•3n+1.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的求和方法:裂项相消求和和错位相减法,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
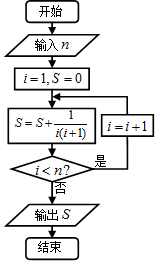
| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com