
分析 (1)直接由已知可得b2,c2,b3,c3的值;
(2)由an+1=an,a1=4,得${a_n}=4({n∈{N^*}})$,然后分别求出bn+1,cn+1,可得${c_{n+1}}-{b_{n+1}}=\frac{1}{2}({{b_n}-{c_n}})=-\frac{1}{2}({{c_n}-{b_n}})$,即数列{cn-bn}是首项为2,公比为$-\frac{1}{2}$的等比数列,由等比数列的通项公式可得数列{cn-bn}的通项公式;
(3)由(2)知,${b_{n+1}}+{c_{n+1}}=\frac{1}{2}({{b_n}+{c_n}})+4$,即${b_{n+1}}+{c_{n+1}}-8=\frac{{{b_n}+{c_n}}}{2}-4=\frac{1}{2}({{b_n}+{c_n}-8})$,结合b1+c1-8=0,可得bn+cn-8=0恒成立,即bn+cn为定值8.
解答 (1)解:由已知可得${b_2}=\frac{9}{2},{c_2}=\frac{7}{2},{b_3}=\frac{15}{4},{c_3}=\frac{17}{4}$;
(2)解:∵an+1=an,a1=4,∴${a_n}=4({n∈{N^*}})$,
∴${b_{n+1}}=\frac{{{a_n}+{c_n}}}{2}=\frac{{4+{c_n}}}{2}=\frac{c_n}{2}+2,{c_{n+1}}=\frac{{{a_n}+{b_n}}}{2}=\frac{b_n}{2}+2$,
则${c_{n+1}}-{b_{n+1}}=\frac{1}{2}({{b_n}-{c_n}})=-\frac{1}{2}({{c_n}-{b_n}})$,
即数列{cn-bn}是首项为2,公比为$-\frac{1}{2}$的等比数列,
∴${c_n}-{b_n}=2•{({-\frac{1}{2}})^{n-1}}$;
(3)证明:由(2)知,${b_{n+1}}+{c_{n+1}}=\frac{1}{2}({{b_n}+{c_n}})+4$,
∴${b_{n+1}}+{c_{n+1}}-8=\frac{{{b_n}+{c_n}}}{2}-4=\frac{1}{2}({{b_n}+{c_n}-8})$,
而b1+c1-8=0,
∴由上述递推关系可得,当n∈N*时,bn+cn-8=0恒成立,
即bn+cn为定值8.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
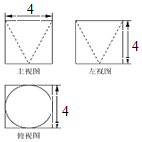
| A. | $8-\frac{2π}{3}$ | B. | $64-\frac{16π}{3}$ | C. | $8-\frac{π}{3}$ | D. | $64-\frac{12π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18km,速度为1 000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1km,参考数据:$\sqrt{3}$≈1.732)( )
如图,飞机的航线和山顶在同一个铅垂面内,若飞机的高度为海拔18km,速度为1 000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1km,参考数据:$\sqrt{3}$≈1.732)( )| A. | 11.4 km | B. | 6.6 km | C. | 6.5 km | D. | 5.6 km |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| z | 0 | 1 | 2 | 3 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com