

分析 (Ⅰ)连结BD,交EF于O,连结OP,推导出EF⊥BD,PO⊥EF,由此能证明EF⊥平面PBD.
(Ⅱ)连结OM,求出cos$∠MOD=\frac{\sqrt{6}}{3}$,sin∠MOD=$\frac{\sqrt{3}}{3}$,cos∠PDO=$\frac{3}{\sqrt{10}}$,sin∠PDO=$\frac{1}{\sqrt{10}}$,从而sin∠OMD=sin(∠MOD+∠MDO)=$\frac{3\sqrt{3}+\sqrt{6}}{3\sqrt{10}}$,由正弦定理得$\frac{MD}{sin∠MOD}=\frac{OD}{sin∠OMD}$,从而求出MD=$\frac{9\sqrt{5}-3\sqrt{10}}{7}a$,PM=$\frac{3\sqrt{10}-2\sqrt{5}}{7}a$,由此能求出λ.
解答 证明:(Ⅰ)连结BD,交EF于O,连结OP,
∵边长为2a的正方形ABCD中,点E,F分别为边AB,BC的中点,
∴EF⊥BD,
又沿DE,DF将△ADE,△DCF折起,使得A,C两点重合于一点P,∴EP=FP,
∵OE=OF,∴PO⊥EF,
∵PO∩BD=O,∴EF⊥平面PBD.
解:(Ⅱ)连结OM,∵OM?平面PBD,EF⊥平面PBD,∴EF⊥OM,
∴∠MOD是平面MEF与平面DEF所成角,
∵平面MEF与平面DEF所成角的余弦值为$\frac{\sqrt{6}}{3}$,
∴cos$∠MOD=\frac{\sqrt{6}}{3}$,sin$∠MOD=\sqrt{1-\frac{2}{3}}$=$\frac{\sqrt{3}}{3}$,
OD=$\frac{3}{4}BD=\frac{3}{4}\sqrt{4{a}^{2}+4{a}^{2}}$=$\frac{3\sqrt{2}}{2}a$,
EF=$\sqrt{2}a$,PE=PF=a,∴PO=$\sqrt{{a}^{2}-\frac{{2a}^{2}}{4}}$=$\frac{\sqrt{2}a}{2}$,$PD=\sqrt{\frac{2}{4}{a}^{2}+\frac{18}{4}{a}^{2}}$=$\sqrt{5}a$,
∴cos∠PDO=$\frac{OD}{PD}$=$\frac{\frac{3\sqrt{2}}{2}a}{\sqrt{5}a}$=$\frac{3}{\sqrt{10}}$,sin∠PDO=$\sqrt{1-\frac{9}{10}}$=$\frac{1}{\sqrt{10}}$,
∴sin∠OMD=sin(∠MOD+∠MDO)
=$\frac{\sqrt{3}}{3}×\frac{3}{\sqrt{10}}+\frac{\sqrt{6}}{3}×\frac{1}{\sqrt{10}}$=$\frac{3\sqrt{3}+\sqrt{6}}{3\sqrt{10}}$,
∵$\frac{MD}{sin∠MOD}=\frac{OD}{sin∠OMD}$,
∴MD=$\frac{\frac{3\sqrt{2}}{2}a×\frac{\sqrt{3}}{3}}{\frac{3\sqrt{3}+\sqrt{6}}{3\sqrt{10}}}$=$\frac{9\sqrt{5}-3\sqrt{10}}{7}a$,
PM=$\sqrt{5}a$-$\frac{9\sqrt{5}-3\sqrt{10}}{7}$a=$\frac{3\sqrt{10}-2\sqrt{5}}{7}a$,
∵$\overrightarrow{PM}$=λ$\overrightarrow{PD}$(0≤λ≤1),
∴λ=$\frac{\overrightarrow{PM}}{\overrightarrow{PD}}$=$\frac{\frac{3\sqrt{10}-2\sqrt{5}}{7}a}{\sqrt{5}a}$=$\frac{3\sqrt{2}-2}{7}$.
点评 本题考查垂直的证明,考查两线段的比值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想,函数与方程思想、数形结合思想,是中档题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
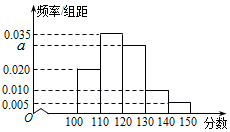 某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.
某校从高三年级中随机选取200名学生,将他们的一模数学成绩绘制成频率分布直方图(如图).由图中数据可知a=0.030.若要从成绩在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从成绩在[130,140)内的学生中选取的人数应为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{2π}{3}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{2π}{3}$,π) | D. | (0,$\frac{π}{3}$]∪[$\frac{2π}{3}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
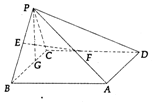 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com