
【题目】已知圆O:![]() ,直线l:
,直线l:![]() .
.
![]() 若直线l与圆O交于不同的两点A、B,当
若直线l与圆O交于不同的两点A、B,当![]() 为锐角时,求k的取值范围;
为锐角时,求k的取值范围;
![]() 若
若![]() ,P是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,则直线CD是否过定点?若是,求出定点,并说明理由.
,P是直线l上的动点,过P作圆O的两条切线PC、PD,切点为C、D,则直线CD是否过定点?若是,求出定点,并说明理由.
![]() 若EF、GH为圆O的两条相互垂直的弦,垂足为
若EF、GH为圆O的两条相互垂直的弦,垂足为![]() ,求四边形EGFH的面积的最大值.
,求四边形EGFH的面积的最大值.
【答案】(1)![]() 或
或![]() ;(2)直线CD恒过定点
;(2)直线CD恒过定点![]() .详见解析(3)
.详见解析(3)![]()
【解析】
(1)首先可以设出![]() 两点坐标,然后联立圆与直线方程并得出
两点坐标,然后联立圆与直线方程并得出![]() 的值,最后根据
的值,最后根据![]() 以及
以及![]() 即可得出结果;
即可得出结果;
(2)首先将![]() 带入直线方程得出直线的解析式,然后设出
带入直线方程得出直线的解析式,然后设出![]() 点坐标并写出以
点坐标并写出以![]() 为直径的圆的方程,最后将其与圆
为直径的圆的方程,最后将其与圆![]() 方程联立即可得出直线
方程联立即可得出直线![]() 的方程并根据直线
的方程并根据直线![]() 的方程得出定点坐标;
的方程得出定点坐标;
(3)首先可以设圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() 、
、![]() ,然后通过勾股定理即可得出
,然后通过勾股定理即可得出![]() 的值,再然后写出
的值,再然后写出![]() 与
与![]() ,通过
,通过![]() 即可求出四边形
即可求出四边形![]() 的面积的最大值。
的面积的最大值。
(1)根据题意,设![]() ,
,![]() ,
,
将![]() 代入
代入![]() ,整理得到:
,整理得到:![]() ,
,
则有![]() ,解可得:
,解可得:![]() ,
,
而![]() ,
,
![]() 为锐角
为锐角![]() ,
,
又由![]() ,
,
解可得:![]() ,
,
又由![]() ,则
,则![]() ,
,
解可得:![]() 或
或![]() ;
;
(2)![]() 时,直线l的方程为:
时,直线l的方程为:![]() ,
,
设![]() ,则以
,则以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,
,
即![]() ,将其和圆O:
,将其和圆O:![]() 联立,消去平方项得:
联立,消去平方项得:![]() ,即为直线
,即为直线![]() 的方程,
的方程,
将其化为![]() 知该直线恒过定点
知该直线恒过定点![]() ,
,
故直线CD恒过定点![]() ;
;
(3)设圆心O到直线EF、GH的距离分别为![]() 、
、![]() ,
,
则![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
当且仅当![]() 即
即![]() 时,取“
时,取“![]() ”,
”,
所以四边形EGFH的面积的最大值为![]() 。
。


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】如图,摄影爱好者在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为![]() ,已知摄影爱好者的身高约为
,已知摄影爱好者的身高约为![]() 米(将眼睛S距地面的距离SA按
米(将眼睛S距地面的距离SA按![]() 米处理).
米处理).
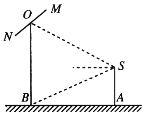
(1)求摄影爱好者到立柱的水平距离AB和立柱的高度OB;
(2)立柱的顶端有一长为2米的彩杆MN,且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转.在彩杆转动的任意时刻,摄影爱好者观察彩杆MN的视角![]() (设为
(设为![]() )是否存在最大值?若存在,请求出
)是否存在最大值?若存在,请求出![]() 取最大值时
取最大值时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解毕业班学业水平考试学生的数学考试情况,抽取了该校100名学生的数学成绩,将所有数据整理后,画出了样频率分布直方图(所图所示),若第1组第9组的频率各为x.

(1)求x的值,并估计这次学业水平考试数学成绩的众数;
(2)若全校有1500名学生参加了此次考试,估计成绩在[80,100)分内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(![]() )①前
)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由.②通项公式为
是否是“回归数列”?并请说明理由.②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(![]() )设
)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值.
的值.
(![]() )是否对任意的等差数列
)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒中装有编号分别为1,2,3,4的四个形状大小完全相同的小球.
(1)从盒中任取两球,求取出的球的编号之和大于5的概率.
(2)从盒中任取一球,记下该球的编号![]() ,将球放回,再从盒中任取一球,记下该球的编号
,将球放回,再从盒中任取一球,记下该球的编号![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C分别为△ABC的三边a,b,c所对的角,向量![]() =(sin A,sin B),
=(sin A,sin B),![]() =(cos B,cos A),且
=(cos B,cos A),且![]() =sin 2C.
=sin 2C.
(1)求角C的大小;
(2)若sin A,sin C,sin B成等差数列,且![]() ,求边c的长.
,求边c的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com