Question

2．如图，在直角坐标系中，△ABC是以（2，1）为圆心，1为半径的圆的内接正三角形，M、N分别是边AC、AB的中点，$\overrightarrow{OM}$•$\overrightarrow{ON}$的取值范围是[$\frac{39-4\sqrt{5}}{8}$，$\frac{39+4\sqrt{5}}{8}$]．

Answer 1

分析 根据条件可求出△ABC的边长为$\sqrt{3}$，可设MN的中点为E，外接圆的圆心为H（2，1），这样根据直角三角形的边角关系即可得出$OH=\sqrt{5}，EH=\frac{1}{4}，EM=\frac{\sqrt{3}}{4}$．根据向量加法的几何意义便可得到$\overrightarrow{OM}•\overrightarrow{ON}=|\overrightarrow{OE}{|}^{2}-\frac{3}{16}$，从而要求$\overrightarrow{OM}•\overrightarrow{ON}$的范围，求出$|\overrightarrow{OE}|$的最大、最小值即可，根据图形可以求出$|\overrightarrow{OE}|$的最值，从而可以得出$\overrightarrow{OM}•\overrightarrow{ON}$的取值范围．

解答 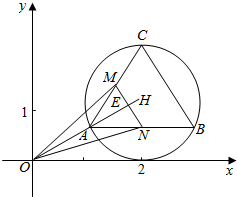解：∵△ABC为正三角形，且外接圆半径为1，∴其边长为$\sqrt{3}$；
如图，连接MN，取MN的中点为E，设外接圆的圆心为H（2，1），则：
连接OH，AH，由条件及几何关系得：$OH=\sqrt{5}，EH=\frac{1}{4}，EM=\frac{\sqrt{3}}{4}$；
$\overrightarrow{OM}=\overrightarrow{OE}+\overrightarrow{EM}，\overrightarrow{ON}=\overrightarrow{OE}-\overrightarrow{EM}$；
∴$\overrightarrow{OM}•\overrightarrow{ON}=|\overrightarrow{OE}{|}^{2}-|\overrightarrow{EM}{|}^{2}$=$|\overrightarrow{OE}{|}^{2}-\frac{3}{16}$；
∴$|\overrightarrow{OE}|$最大时，$\overrightarrow{OM}•\overrightarrow{ON}$最大，$|\overrightarrow{OE}|$最小时，$\overrightarrow{OM}•\overrightarrow{ON}$最小；
根据图形可看出，当OH的连线经过A点，且A点在线段OH上时$|\overrightarrow{OE}|$最小，A点在线段OH的延长线上时，$|\overrightarrow{OE}|$最大；
∴可求得$|\overrightarrow{OE}|$的最小值为$\sqrt{5}-\frac{1}{4}$，最大值为$\sqrt{5}+\frac{1}{4}$；
∴$\overrightarrow{OM}•\overrightarrow{ON}$的最小值为$（\sqrt{5}-\frac{1}{4}）^{2}-\frac{3}{16}=\frac{39-4\sqrt{5}}{8}$，最大值为$\frac{39+4\sqrt{5}}{8}$；
∴$\overrightarrow{OM}•\overrightarrow{ON}$的范围为$[\frac{39-4\sqrt{5}}{8}，\frac{39+4\sqrt{5}}{8}]$．
故答案为：[$\frac{39-4\sqrt{5}}{8}$，$\frac{39+4\sqrt{5}}{8}$]．

点评 考查三角形外接圆的定义，直角三角形的边角关系，向量加法的几何意义，相反向量的概念，以及数量积的运算，通过观察图形便能看出$|\overrightarrow{OE}|$何时取到最值．