Question

1．设f（x）=$\frac{mx}{1+|x|}$，集合N={y|y=f（x），x∈[a，b]}，若使得N=[a，b]的实数对（a，b）（a＜b）恰好有3个，则实数m的取值范围是m＞1．

Answer 1

分析 由题意判断函数f（x）=$\frac{mx}{1+|x|}$的奇偶性与单调性，从而转化为函数的图象的交点的个数问题，从而结合图象解得．

解答 解：令y=$\frac{x}{1+|x|}$，
易知y=$\frac{x}{1+|x|}$在R上是奇函数且单调递增，
当m＜0时，
f（x）=$\frac{mx}{1+|x|}$在R上是减函数且是奇函数，
若N={y|y=f（x），x∈[a，b]}=[a，b]，
则f（a）=b，且f（b）=a，
由点（a，b）与点（b，a）关于y=x对称，
则a＜0＜b，
∴f（-a）=-f（a）=-b，
若b＜-a，则f（b）＞f（-a），a＞-b，-a＜b矛盾，
若b＞-a，则f（b）＜f（-a），a＜-b，-a＞b矛盾，
故b=-a，
故f（x）=-x的非零解，
即f（x）与直线y=-x的非零交点的个数，
结合图象可知，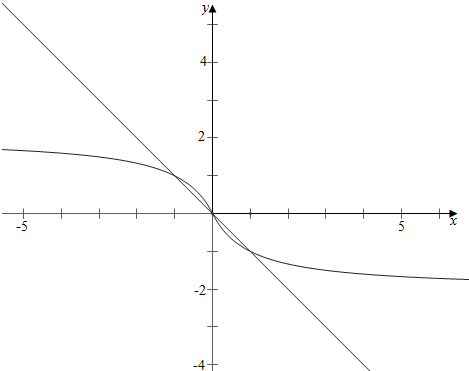
，
最多有一对非零交点，故不成构成3对；
当m=0时，显然不成立；
当m＞0时，同理可化为f（x）与直线y=x的交点的个数，
结合图象可知，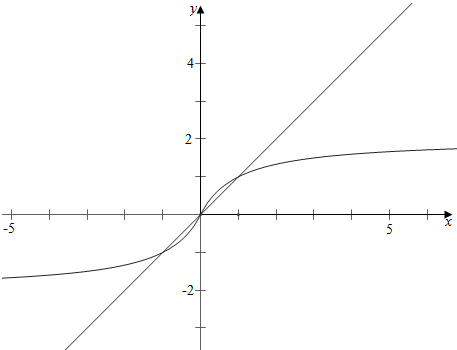

由方程$\frac{mx}{1+|x|}$=x知，
当m＞1时，有三个交点，
可构成3对（a，b）；
当0＜m≤1时，不能构成3对（a，b）；
故答案为：m＞1．

点评 本题考查了函数的性质的判断与应用，同时考查了数形结合的思想应用．