Question

16．已知点A，B分别为异面直线a，b上的点，且直线AB与a，b均垂直，动点P∈a，Q∈b，PA+QB为定值，则线段PQ中点M的轨迹是（　　）

• A． 平行四边形
• B． 圆
• C． 椭圆
• D． 双曲线

Answer 1

分析 作直线a，b以及点P、Q在线段AB的中垂面上的投影，记为直线a′，b′认及点P′，Q′，由线段P′Q′的中点即为点M，这样把空间问题转化成平面问题．

解答 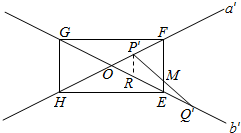解：如图，作直线a，b以及点P、Q在线段AB的中垂面上的投影，
记为直线a′，b′认及点P′，Q′，由线段P′Q′的中点即为点M，
设FA+QB=2m，而OE=OF=OG=OH=m，
以P′，Q′分别在射线OF，OE上为例，
由OP′+OQ′=AP+BQ=2m，OE+OF=2m，
得FP′=EQ′，
过P′作EF的平行线交直线b′与点R，
则有FP′=ER=EQ′，
∴线段P′Q′的中点M在线段EF上，
类似的，可得其情形时点M的轨迹分别为线段FG，GH，HE，
综上，线段PQ的中点M的轨迹是矩形EFGH．
故选：A．

点评 本题考查点的轨迹的判断，是中档题，解题时要认真审题，合理地化空间问题为平面问题，注意数形结合思想的合理运用．