
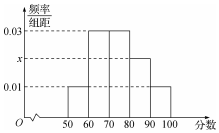
 2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).分析 (1)由频率分布直方图求出第4组的频率,从而得到x=0.02,从而可估计所抽取的50名学生成绩的平均数和中位数.
(2)先求出50名学生中成绩不低于70分的频率为0.6,由此可以估计高三年级2000名学生中成绩不低于70分的人数.
(3)三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在[70,80)这组的3名学生分别为a,b,c,成绩在[80,90)这组的2名学生分别为d,e,成绩在[90,100]这组的1名学生为f由此利用列举法能求出从中任抽取3人,[80,90),[90,100]两组中至少有1人被抽到的概率.
解答 解:(1)由频率分布直方图可得第4组的频率为1-0.1-0.3-0.3-0.1=0.2,
故x=0.02.
故可估计所抽取的50名学生成绩的平均数为(55×0.01+65×0.03+75×0.03+85×0.02+95×0.01)×10=74(分).
由于前两组的频率之和为0.1+0.3=0.4,前三组的频率之和为0.1+0.3+0.3=0.7,故中位数在第3组中.
设中位数为t分,
则有(t-70)×0.03=0.1,所以$t=73\frac{1}{3}$,
即所求的中位数为$73\frac{1}{3}$分.
(2)由(1)可知,50名学生中成绩不低于70分的频率为0.3+0.2+0.1=0.6,
由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为2000×0.6=1200.
(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.
记成绩在[70,80)这组的3名学生分别为a,b,c,成绩在[80,90)这组的2名学生分别为d,e,
成绩在[90,100]这组的1名学生为f,
则从中任抽取3人的所有可能结果为:
(a,b,c),(a,b,d),(a,b,e),(a,b,f),(a,c,d),(a,c,e),(a,c,f),(a,d,e),
(a,d,f),(a,e,f),(b,c,d),(b,c,e),(b,c,f),(b,d,e),(b,d,f),(b,e,f),
(c,d,e),(c,d,f),(c,e,f),(d,e,f)共20种.
其中[80,90),[90,100]两组中没有人被抽到的可能结果为(a,b,c),只有1种,
故[80,90),[90,100]两组中至少有1人被抽到的概率为$P=1-\frac{1}{20}=\frac{19}{20}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x}$ | B. | y=tanx | C. | $y=x+\frac{1}{x}$ | D. | y=ex-e-x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{18}{20}$ | C. | $\frac{112}{125}$ | D. | $\frac{17}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 40 | C. | -40 | D. | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com