
(本小题满分13分)在平面直角坐标系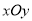 中,椭圆
中,椭圆 过点
过点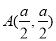 和点
和点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点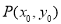 在椭圆
在椭圆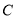 上,
上,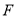 为椭圆的左焦点,直线
为椭圆的左焦点,直线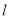 的方程为
的方程为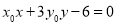 .
.
(i)求证:直线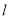 与椭圆
与椭圆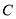 有唯一的公共点;
有唯一的公共点;
(ii)若点 关于直线
关于直线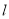 的对称点为
的对称点为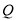 ,探索:当点
,探索:当点 在椭圆
在椭圆 上运动时,直线
上运动时,直线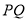 是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
(1)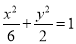 ;(2)(i)详见解析;(ii)定点坐标为
;(2)(i)详见解析;(ii)定点坐标为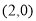 .
.
【解析】
试题分析:(1)根据题意,将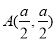 和点
和点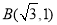 分别代入椭圆方程,即可得到关于
分别代入椭圆方程,即可得到关于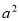 ,
,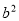 的方程组:
的方程组: ,
,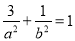 ,从而可以解得
,从而可以解得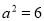 ,
,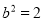 ,即椭圆
,即椭圆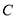 的方程为
的方程为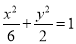 ;(2)(ii)分析题意可知,要证直线
;(2)(ii)分析题意可知,要证直线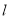 与椭圆
与椭圆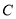 只有一个公共点,等价于将直线方程与椭圆方程联立所得的方程组只有唯一的解,因此考虑将方程联立,化简变形可得
只有一个公共点,等价于将直线方程与椭圆方程联立所得的方程组只有唯一的解,因此考虑将方程联立,化简变形可得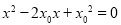 ,易知其
,易知其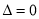 ,从而得证;(ii)由题意可知
,从而得证;(ii)由题意可知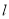 为线段
为线段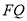 的中垂线,因此利用线段
的中垂线,因此利用线段 与直线
与直线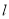 垂直以及线段
垂直以及线段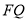 的中点在直线
的中点在直线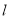 上可求得点
上可求得点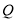 的坐标为
的坐标为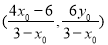 ,以下需分类讨论列出直线
,以下需分类讨论列出直线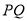 的解析式:当
的解析式:当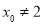 时,直线
时,直线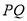 的斜率
的斜率 ,直线
,直线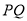 的方程为
的方程为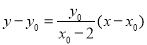 ,即
,即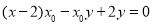 ,直线过定点
,直线过定点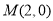 ,当
,当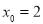 时,
时,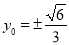 ,此时
,此时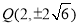 ,直线
,直线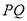 过点
过点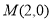 ,即可证明直线
,即可证明直线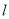 恒过定点
恒过定点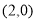 .
.
试题解析:(1)∵ ,且
,且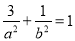 ,∴
,∴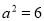 ,
,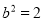 ,∴椭圆
,∴椭圆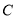 的方程为
的方程为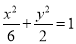 .
.
(2)(i)联立方程组 ,整理为
,整理为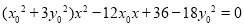 …①,
…①,
∵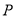 在椭圆
在椭圆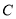 上,∴
上,∴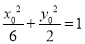 ,即
,即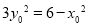 ,∴方程①为
,∴方程①为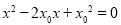 ,即
,即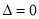 ,∴直线
,∴直线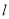 与椭圆
与椭圆 有唯一的公共点; (ii)∵
有唯一的公共点; (ii)∵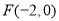 ,∴过点
,∴过点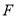 且与
且与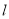 垂直的直线方程为
垂直的直线方程为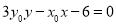 ,
,
∵联立方程组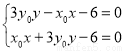 ,∴
,∴ ,∵
,∵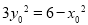 ,且
,且 ,∴
,∴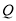 点坐标为
点坐标为 ,当
,当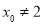 时,直线
时,直线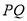 的斜率
的斜率 ,
,
∵直线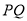 的方程为
的方程为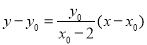 ,即
,即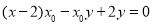 ,∴直线过定点
,∴直线过定点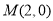 ,
,
当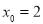 时,
时,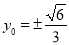 ,此时
,此时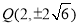 ,直线
,直线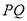 过点
过点 ,综上所述,直线过定点
,综上所述,直线过定点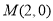 .
.
考点:1.椭圆的标准方程;2.直线与椭圆的位置关系;3.直线中的对称问题.


科目:高中数学 来源:2014-2015学年豫晋冀高三上学期第二次调研考试文科数学试卷(解析版) 题型:选择题
已知F为抛物线 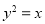 的焦点,点A,B在该抛物线上且位于x轴的两侧,
的焦点,点A,B在该抛物线上且位于x轴的两侧,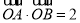 (其中O为坐标原点),则△AFO与△BFO面积之和的最小值是( )
(其中O为坐标原点),则△AFO与△BFO面积之和的最小值是( )
A.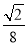 B.
B.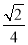 C.
C.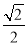 D.
D.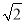
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试文科数学试卷(解析版) 题型:选择题
已知单位向量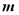 和
和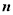 的夹角为
的夹角为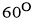 ,记
,记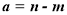 ,
, 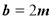 , 则向量
, 则向量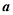 与
与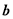 的夹角为 ( )
的夹角为 ( )
(A)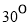 (B)
(B)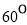 (C)
(C)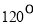 (D)
(D)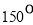
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省宜宾市高三第一次诊断考试理科数学试卷(解析版) 题型:选择题
给出下列三个命题:
①命题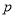 :
: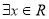 ,使得
,使得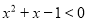 ,则
,则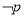 :
: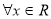 ,使得
,使得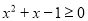
② 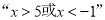 是“
是“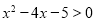 ”的充要条件.
”的充要条件.
③若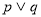 为真命题,则
为真命题,则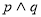 为真命题.
为真命题.
其中正确命题的个数为( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三一诊模拟文科数学试卷(解析版) 题型:选择题
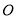 为坐标原点,点
为坐标原点,点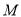 的坐标为
的坐标为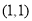 ,若点
,若点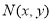 的坐标满足
的坐标满足 ,则
,则 的最
的最
大值为( )
A.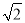 B.
B.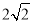 C.
C.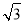 D.
D.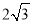
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省高三一诊模拟理科数学试卷(解析版) 题型:填空题
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为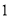 ,则该几何体的体积为 .
,则该几何体的体积为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com