考点:平面与平面平行的判定,异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由条件利用正方体的性质,可得异面直线D1C1与BD所成的角即∠BDC,从而得到答案.
(2)由正方体的性质可得BD∥B1D1,再利用直线和平面平行的判定定理证得 BD∥平面B1D1E.
(3)证明BF∥D1E,利用直线和平面平行的判定定理证得BF∥平面B1D1E.结合(2)的结论以及BF∩BD=B,利用平面和平面平行判定定理证得平面BDF∥平面B1D1E.
解答:
解:(1)正方体ABCD-A1B1C1D1中,由于D1C1∥DC,故异面直线D1C1与BD所成的角即∠BDC,
而∠BDC=45°,∴异面直线D1C1与BD所成的角的大小是45°,
故答案为:45°.
(2)由正方体的性质可得BD∥B1D1,而B1D1?平面B1D1E,BD不在平面B1D1E内,
∴BD∥平面B1D1E.
(3)取DD1的中点M,则D1E∥MA,而MA∥BF,∴BF∥D1E.
而D1E?平面B1D1E,BF不在平面B1D1E中,故有BF∥平面B1D1E.
再由BD∥平面B1D1E,且BF∩BD=B,∴平面BDF∥平面B1D1E.
点评:本题主要考查求异面直线所成的角,直线和平面平行的判定定理、平面和平面平行判定定理的应用,属于基础题.

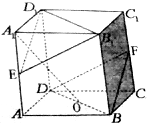 已知正方体ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,则
已知正方体ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,则

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案