
| 甲 | 80 | 81 | 93 | 72 | 88 | 75 | 83 | 84 |
| 乙 | 82 | 93 | 70 | 84 | 77 | 87 | 78 | 85 |
分析 (1)以十位数为茎,个位数为叶,能作出表示这两组数据的茎叶图.
(2)分别求出甲、乙两组数扭的平均数和方差,由于甲乙的平均成绩相等,而甲的方差较小,所以甲的成绩较稳定,派甲参赛比较合适.
(3)由已知条件利用等可能事件概率计算公式能求出该班对甲乙两同学的成绩高于79个/分钟的概率.
解答 解:(1)以十位数为茎,个位数为叶,能作出表示这两组数据的茎叶图: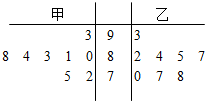
…(4分)
(2)$\overline{x_甲}=\frac{80+81+93+72+88+75+83+84}{8}=82$,
$\overline{x_乙}=\frac{82+93+70+84+77+87+78+85}{8}=82$,
$S_甲^2=\frac{{{2^2}+{1^2}+{{11}^2}+{{10}^2}+{6^2}+{7^2}+{1^2}+{2^2}}}{8}=39.5$,
$S_乙^2=\frac{{{0^2}+{{11}^2}+{{12}^2}+{2^2}+{5^2}+{5^2}+{4^2}+{3^2}}}{8}=43$
由于甲乙的平均成绩相等,而甲的方差较小,所以甲的成绩较稳定,派甲参赛比较合适…(8分)
注:本小题的结论及理由不唯一,如果考生从统计学的角度分析,给出其他合理回答,同样给分;
如派甲比较合适,理由如下:甲获得79个/分钟以上的概率为${P_1}=\frac{6}{8}=\frac{3}{4}$,
乙获得79个/分钟以上的概率为${P_2}=\frac{5}{8}$.∵P1>P2,所以派甲参赛比较合适.
(3)甲获得79个/分钟以上的概率为${P_1}=\frac{6}{8}=\frac{3}{4}$,乙获得79个/分钟以上的概率为${P_2}=\frac{5}{8}$.…(12分)
点评 本题考查概率的求法,考查平均数、方差的性质的应用,考查茎叶图的作法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,0] | B. | [0,$\frac{π}{3}$] | C. | [$\frac{π}{12}$,$\frac{π}{2}$] | D. | [$\frac{π}{2}$,$\frac{5π}{6}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com