Question

【题目】全国文明城市是中国所有城市品牌中含金量最高、创建难度最大的一个，是反映城市整体文明水平的综合性荣誉称号，是目前国内城市综合类评比中的最高荣誉，也是最具价值的城市品牌，作为普通市民，既是城市文明的最大受益者，更是文明城市的主要创造者，皖北某市为提高市民对文明城市创建的认识，举办了“创建文明城市”知识竞赛，从所有答卷中随机抽取400份试卷作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段：后得到如图所示的频率分布直方图.

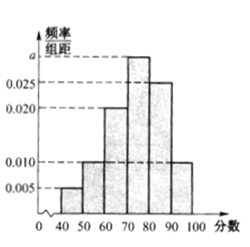
（Ⅰ）求样本的平均数；

（Ⅱ）现从该样本成绩在与两个分数段内的市民中按分层抽样选取6人，求从这6人中随机选取2人，且2人的竞赛成绩之差的绝对值大于20的概率.

Answer 1

【答案】（Ⅰ）74（Ⅱ）

【解析】

（Ⅰ）根据小矩形的面积之和等于可求出，再根据平均数小矩形的面积小矩形底边中点横坐标之和，即可求解.

（Ⅱ）根据分层抽样算出在内选取2人，在内选取4人，利用列举法求出从这6人中选取2人的所有选取方法，再求出2人成绩之差的绝对值大于20的选取方法，利用古典概型的概率计算公式即可求解.

（Ⅰ）因为

所以，

从而样本平均数为

（Ⅱ）根据分层抽样，在内选取2人，记为，

在内选取4人，记为.

从这6人中选取2人的所有选取方法：

，共15种.

2人成绩之差的绝对值大于20的选取方法：

共8种.

所以所求概率为.