
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其准线的距离为2.
到其准线的距离为2.

(1)求抛物线![]() 的方程;
的方程;
(2)如图![]() ,
,![]() ,
,![]() 为抛物线
为抛物线![]() 上三个点,
上三个点,![]() ,若四边形
,若四边形![]() 为菱形,求四边形
为菱形,求四边形![]() 的面积.
的面积.
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]()
【解析】
(1)利用点在抛物线上和焦半径公式列出关于![]() 的方程组求解即可。
的方程组求解即可。
(2)设出A,C点的坐标及直线AC,利用设而不求和韦达定理求出AC中点的坐标,然后求出B点的坐标,利用B在抛物线上以及直线BD和直线AC的斜率互为负倒数列出方程组求出B点坐标,然后求出AC的长度,即可求出面积。
(1)由已知可得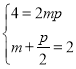 ,
,
消去![]() 得:
得:![]() ,
,![]()
抛物线![]() 的方程为
的方程为![]()
(2)设![]() ,
,![]() ,菱形
,菱形![]() 的中心
的中心![]()
当![]() 轴,则
轴,则![]() 在原点,
在原点,![]() ,
,
![]() ,
,![]() ,菱形的面积
,菱形的面积![]() ,
,
解法一:当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 方程:
方程:![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]()
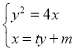 消去
消去![]() 得:
得:![]()

![]()
![]() ,
,![]() ,∵
,∵![]() 为
为![]() 的中点
的中点
∴![]() ,点
,点![]() 在抛物线上,
在抛物线上,
且直线![]() 的斜率为
的斜率为![]() 。
。
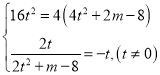 解得:
解得:![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
综上,![]() 或
或![]()
解法二:设![]() ,直线
,直线![]() 的斜率为
的斜率为![]()
![]()
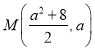 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
可以设直线![]() :
:![]()
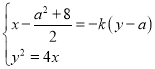 消去
消去![]() 得:
得:![]()
∵![]()
![]() ,
,![]()
解方程:![]() ,解得
,解得![]() ,
,![]() ,接下去同上。
,接下去同上。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线
轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线的参数方程是
,直线的参数方程是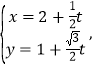 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n为正整数集合![]() ,n对于集合A中的任意元素
,n对于集合A中的任意元素![]() 和
和![]() ,记
,记![]() .
.
(1)当![]() 时,若
时,若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)当![]() 时,设B是A的子集,且满足:对于B中的任意元素α,β,当α,β相同时,
时,设B是A的子集,且满足:对于B中的任意元素α,β,当α,β相同时,![]() 是奇数;当α,β不同时,
是奇数;当α,β不同时,![]() 是偶数.求集合B中元素个数的最值.
是偶数.求集合B中元素个数的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大型综艺节目,《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的![]() 根据调查显示,是否喜欢盲拧魔方与性别有关
根据调查显示,是否喜欢盲拧魔方与性别有关![]() 为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表
为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如表![]() 所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表
所示,并邀请其中20名男生参加盲拧三阶魔方比赛,其完成情况如表![]() 所示.
所示.


(Ⅰ)将表![]() 补充完整,并判断能否在犯错误的概率不超过
补充完整,并判断能否在犯错误的概率不超过![]() 的前提下认为是否喜欢盲拧与性别有关?
的前提下认为是否喜欢盲拧与性别有关?
(Ⅱ)现从表![]() 中成功完成时间在
中成功完成时间在![]() 和
和![]() 这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
这两组内的6名男生中任意抽取2人对他们的盲拧情况进行视频记录,求2人成功完成时间恰好在同一组内的概率.
附参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82,81,79,78,95,88,93,84
乙:92,95,80,75,83,80,90,85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学有着辉煌和灿烂的历史,成书于公元一世纪的数学著作《九章算术》中有一道关于数列的题目:“今有良马与驽马发长安至齐。齐去长安三千里。良马初日行一百九十三里,日增十三里。驽马初日行九十七里,日减半里。良马先至齐,复还迎驽马。问几何日相逢及各行几何?”根据你所学数列知识和数学运算技巧计算两马相逢时是在出发后的第_______天(写出整数即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com