练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．求直线2x+y-6=0与直线2x+y-1=0间的距离为（　　）
    A．7B．5C．$\sqrt{5}$D．$\sqrt{7}$

    分析 运用两平行线Ax+By+C1=0，Ax+By+C2=0，的距离公式d=$\frac{|{C}_{1}-{C}_{2}|}{\sqrt{{A}^{2}+{B}^{2}}}$，代入计算即可得到所求值．

    解答 解：由于直线2x+y-6=0与直线2x+y-1=0平行，
    由两条平行线的距离公式可得：
    所求距离为d=$\frac{|-6+1|}{\sqrt{4+1}}$=$\sqrt{5}$．
    故选：C．

    点评 本题考查两平行线的距离公式的运用，考查运算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．设z=$\frac{（1-4i）（1+i）+2+4i}{3+4i}$．
    ①求|z|；
    ②若$\frac{{|{\overline z}|+mi}}{1-i}=\sqrt{2}$i，m∈R，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知复数z满足（1+2i3）z=1+2i，则z的虚部是$\frac{4}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

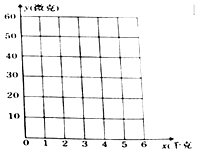    9．菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水x（单位：千克） 清洗该蔬菜1千克后，蔬菜上残留的农药y（单位：微克） 的统计表：
    x12345
     y5854392910
    （1）在下面的坐标系中，描出散点图，并判断变量x与y的相关性；
    （2）若用解析式$\widehaty=c{x^2}+d$作为蔬菜农药残量$\widehaty$与用水量x的回归方程，令ω=x2，计算平均值$\overlineω$与$\overline y$，完成以下表格（填在答题卡中），求出$\widehaty$与x的回归方程．（c，d精确到0.1）
    ω1491625
    y5854392910
    ${ω_i}-\overlineω$-10-7-2514
    ${y_i}-\overline y$20161-28
    （3）对于某种残留在蔬菜上的农药，当它的残留量低于20微克时对人体无害，为了放心食用该蔬菜，请
    估计需要用多少千克的清水清洗一千克蔬菜？（精确到0.1，参考数据$\sqrt{5}≈2.236$）
    （附：线性回归方程$\widehaty=bx+a$中系数计算公式分别为；$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$a=\overline y-b\overline x$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知函数f（x）=x2+2xf'（1），则f'（1）-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知向量$\overrightarrow a$，$\overrightarrow{b}$为两个互相垂直的单位向量，向量$\overrightarrow c$满足$（\overrightarrow a-\overrightarrow c）•（2\overrightarrow b-\overrightarrow c）$=0，则$|\overrightarrow c{|_{max}}$=$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=$\frac{a+lnx}{x}$在点（1，f（1））处的切线与x轴平行．
    （1）求实数a的值及f（x）的极值；
    （2）是否存在区间$（t，t+\frac{2}{3}）$（t＞0），使得f（x）在此区间上存在极值点和零点？若存在，求出实数t的取值范围，若不存在，请说明理由；
    （3）如果对任意x1、x2∈[e2，+∞]，有|f（x1）-f（x2）|≥k|$\frac{1}{x_1}-\frac{1}{x_2}$|，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．椭圆的中心在坐标原点，焦点在x轴上，左右顶点分别为A1、A2，上下顶点分别为B1、B2，F2为右焦点，延长B2F2与A2B1交于点P，若∠B2PA2为钝角，则该椭圆离心率的取值范围是（　　）
    A．$（{\frac{{\sqrt{5}-2}}{2}，0}）$B．$（{0，\frac{{\sqrt{5}-2}}{2}}）$C．$（{0，\frac{{\sqrt{5}-1}}{2}}）$D．$（{\frac{{\sqrt{5}-1}}{2}，1}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．在二项式（x2-$\frac{1}{2x}$）9的展开式中，第4项的二项式系数是84．

    查看答案和解析>>

    同步练习册答案