
 菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克) 清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克) 的统计表:
菜农定期使用低害杀虫农药对蔬菜进行喷洒,以防止害虫的危害,但采集上市时蔬菜仍存有少量的残留农药,食用时需要用清水清洗干净,下表是用清水x(单位:千克) 清洗该蔬菜1千克后,蔬菜上残留的农药y(单位:微克) 的统计表:| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ${ω_i}-\overlineω$ | -10 | -7 | -2 | 5 | 14 |
| ${y_i}-\overline y$ | 20 | 16 | 1 | -28 |
分析 (1)根据题意描出散点图,根据散点图判断变量x与y的相关性;
(2)计算$\overline{ω}$、$\overline{y}$,填表即可,求出回归系数,写出回归方程;
(3)求$\widehaty<20$时x的取值范围即可.
解答 解:(1)在下面的坐标系中,描出散点图如图所示,
根据散点图知变量x与y负相关;
(2)计算$\overline{ω}$=$\frac{1}{5}$×(12+22+32+42+52)=11,
$\overline{y}$=$\frac{1}{5}$×(58+54+39+29+10)=38;
填表如下;
| ω | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ${ω_i}-\overlineω$ | -10 | -7 | -2 | 5 | 14 |
| ${y_i}-\overline y$ | 20 | 16 | 1 | -9 | -28 |
点评 本题考查了非线性相关的二次拟合问题,也考查了线性回归方程的计算问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | 年龄为37岁的人体内脂肪含量都为20.90% | |
| B. | 年龄为37岁的人体内脂肪含量为21.01% | |
| C. | 年龄为37岁的人群中的大部分人的体内脂肪含量为20.90% | |
| D. | 年龄为37岁的大部分的人体内脂肪含量为31.50% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
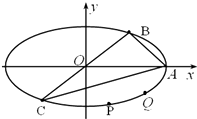 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,点A,B,C为椭圆上的三个点,A为椭圆的右端点,BC过中心O,且|BC|=2|AB|,S△ABC=3.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为4,点A,B,C为椭圆上的三个点,A为椭圆的右端点,BC过中心O,且|BC|=2|AB|,S△ABC=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
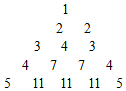 观察如图所示的”三角数阵”
观察如图所示的”三角数阵”查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 圆台侧面的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面半径的2倍.求两底面的面积之和是( )
圆台侧面的母线长为2a,母线与轴的夹角为30°,一个底面的半径是另一个底面半径的2倍.求两底面的面积之和是( )| A. | 3πa2 | B. | 4πa2 | C. | 5πa2 | D. | 6πa2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com