
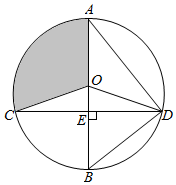
 如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.分析 (1)根据圆周角定理,以及三角形全等即可证明.
(2)由⊙O的直径AB垂直于弦CD于E,利用垂径定理可得CE=ED.在Rt△ABD中,利用直角三角形的边角关系可得BD=ABsin∠BAD.再利用勾股定理可得.由等面积变形可得,即可得出.
解答  证明:(1)因为AB是⊙O的直径,AB⊥CD,
证明:(1)因为AB是⊙O的直径,AB⊥CD,
所以$\widehat{CB}$=$\widehat{BD}$,$\widehat{AC}$=$\widehat{AD}$,所以∠BAD=∠CDB,…(2分)
∠AOC=∠AOD.因为AO=DO,所以∠BAD=∠ADO,
所以∠CDB=∠ADO.…(5分)
(2)因为AB是⊙O的直径,OD=5
所以∠ADB=90°,AB=10
在Rt△ABD中,$sin∠BAD=\frac{BD}{AB}$
又$sin∠BAD=\frac{3}{5}$,所以$\frac{BD}{10}=\frac{3}{5}$,
所以BD=6.…(7分)$AD=\sqrt{A{B^2}-B{D^2}}=\sqrt{{{10}^2}-{6^2}}=8$
因为∠ADB=90°,AB⊥CD
所以$DE\cdotAB=AD\cdotBD,CE=DE$
所以DE×10=8×6
所以$DE=\frac{24}{5}$,所以$CD=2DE=\frac{48}{5}$.…(10分)
点评 本题综合考查了圆的性质、垂径定理、直角三角形的边角关系、勾股定理、等面积变形、三角形外角定理、扇形的面积计算公式等基础知识与基本技能方法,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 分层抽样、分层抽样、抽签法、系统抽样 | |
| B. | 分层抽样、分层抽样、随机数法、系统抽样 | |
| C. | 抽签法、分层抽样、随机数法、系统抽样 | |
| D. | 抽签法、分层抽样、系统抽样、随机数法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{13}}{2}$S | B. | $\frac{3}{2}$S | C. | S | D. | $\frac{1}{2}$S |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com