
| A. | (-3,0) | B. | (-∞,0) | C. | (-∞,-3) | D. | (0,+∞) |
分析 先判断a<0,再分析x<0,函数在x=$\frac{a}{3}$时取得极大值-$\frac{{a}^{3}}{27}$-1,x=0时取得极小值-1,利用f(x)=$\left\{\begin{array}{l}{2{x}^{3}-a{x}^{2}-1,x<0}\\{|x-3|+a,x≥0}\end{array}\right.$恰有2个零点,即可得出结论.
解答 解:由题意,a<0,
x<0,f(x)=2x3-ax2-1,
f′(x)=2x(3x-a)=0,可得x=0或$\frac{a}{3}$,
∴函数在x=$\frac{a}{3}$时取得极大值-$\frac{{a}^{3}}{27}$-1,x=0时取得极小值-1,
∵函数f(x)=$\left\{\begin{array}{l}{2{x}^{3}-a{x}^{2}-1,x<0}\\{|x-3|+a,x≥0}\end{array}\right.$恰有两个零点,
∴-$\frac{{a}^{3}}{27}$-1<0且3+a>0
∴-3<a<0,
故选:A.
点评 本题考查分段函数,考查函数的零点,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | -1 | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p的逆命题为“若a>b,则lga>lgb”,且该命题为假命题 | |
| B. | 命题p的否命题为“若lga>lgb,则a≤b”,且该命题为真命题 | |
| C. | 命题p的逆否命题为“若a≤b,则lga≤lgb”,且该命题为真命题 | |
| D. | 命题p的否定为“若lga≤lgb,则a≤b”,且该命题为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
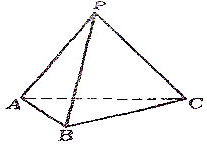 如图,点P是△ABC在平面外的一点,PA=PB=PC=2,AB=BC=AC=1,
如图,点P是△ABC在平面外的一点,PA=PB=PC=2,AB=BC=AC=1,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com