
分析 对每个命题分别进行判断,即可得出结论.
解答 解:①α≠90°时,每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应,故不正确;
②倾斜角的范围是:0°≤α<180°,0°≤α<90,当倾斜角增大时,斜率也增大;90°<α<180°,当倾斜角增大时,斜率也增大,故不正确;
③m≠1时过两点A(1,2),B(m,-5)的直线可以用两点式表示,故不正确;
④过点(1,1),且斜率为1的直线的方程为$\frac{y-1}{x-1}$=1(x≠1),故不正确;
⑤直线Ax+By+C=0(A,B不同时为零),当A,B,C中有一个为零时,这个方程不能化为截距式,正确.
⑥斜率存在时,若两直线垂直,则它们的斜率相乘必等于-1,故不正确.
故答案为:⑤.
点评 本题考查命题的真假判断,考查直线的斜率、倾斜角、直线的方程,属于中档题.


科目:高中数学 来源: 题型:解答题
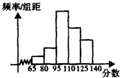 为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.
为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.41,0.03 | B. | 0.56,0.03 | C. | 0.41,0.15 | D. | 0.56,0.15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{{3+{{(-1)}^n}}}{2}$ | B. | ${a_n}=\frac{{3+{{(-1)}^{n+1}}}}{2}$ | ||
| C. | ${a_n}=\frac{3+cosnπ}{2}$ | D. | ${a_n}=\frac{{3+sin\frac{2n+1}{2}π}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com