
分析 (1)甲同学不能站在正中间,因而先排甲同学,然后再排其余六名同学,问题得以解决.
(2)甲、乙两名同学不站在两端,因而先排甲、乙两同学,然后再排其余五名同学,问题得以解决.
(3)甲、乙两名同学不能相邻,因而先排除甲、乙两名同学外的其余五名同学,然后再从六个空里选两个空插入甲、乙两名同学,问题得以解决.
(4)定序法,甲乙的顺序只有两种,7名同学站成一排,排法数为$A_7^7$,问题得以解决.
解答 解:(1)甲同学不能站在正中间,因而先排甲同学,然后再排其余六名同学,满足条件的排法数为$A_6^1A_6^6=4320$ 种;
(2)甲、乙两名同学不站在两端,因而先排甲、乙两同学,然后再排其余五名同学,满足条件的排法数为$A_5^2A_5^5=2400$ 种;
(3)甲、乙两名同学不能相邻,因而先排除甲、乙两名同学外的其余五名同学,然后再从六个空里选两个空插入甲、乙两名同学,满足条件的排法数为$A_5^5A_6^2=3600$ 种;
(4)甲同学必须站在乙同学的左边(不一定相邻),7 名同学站成一排,排法数为$A_7^7$,其中甲同学站在乙同学的左边和乙同学站在甲同学的左边(不一定相邻)的情况一一对应,
各占其半,故满足条件的排法总数为$\frac{A_7^7}{2}$=2520种.
点评 本题考查排列、组合的应用,注意特殊问题的处理方法,如相邻用捆绑法,不能相邻用插空法,定序法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 232种 | B. | 252种 | C. | 256种 | D. | 472种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
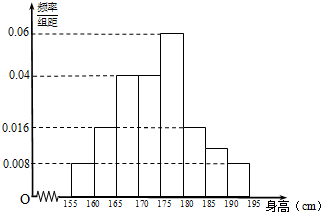 从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如.
从某校高一年级800名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米和195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com