练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．98和63的最大公约数为7．

    分析 本题考查的知识点是辗转相除法，根据辗转相除法的步骤，将98和63代入易得到答案．

    解答 解：98=63×1+35，
    63=35×1+28，
    35=28×1+7，
    28=7×4，
    故98和63的最大公约数为7，
    故答案为：7

    点评 对任意整数a，b，b＞0，存在唯一的整数q，r，使a=bq+r，其中0≤r＜b，这个事实称为带余除法定理，若c|a，c|b，则称c是a，b的公因数．若d是a，b的公因数，且d可被a，b的任意公因数整除则称d是a，b的最大公因数．当d≥0时，d是a，b公因数中最大者．若a，b的最大公因数等于1，则称a，b互素．累次利用带余除法可以求出a，b的最大公因数，这种方法常称为辗转相除法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．从{-3，-2，-1，0，1，2，3}中，任取3个不同的数作为抛物线的方程y=ax2+bx+c（a≠0）的系数，使抛物线过原点，且顶点在第一象限这样的抛物线共有（　　）条．
    A．9B．6C．12D．7

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=log2（x+2）与g（x）=（x-a）2+1，若对任意的x1∈[2，6），都存在x2∈[0，2]，使得f（x1）=g（x2），则实数a的取值范围是[-1，2-$\sqrt{2}$]∪[$\sqrt{2}$，3]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知曲线C的参数方程为$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$（t为参数）（p＞0），直线l经过曲线C外一点A（-2，-4）且倾斜角为$\frac{π}{4}$．
    （1）求曲线C的普通方程和直线l的参数方程；
    （2）设直线l与曲线C分别交于M1，M2，若|AM1|，|M1M2|，|AM2|成等比数列，求p的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知关于某设各的使用年限x（单位：年）和所支出的维修费用y（单位：万元）有如下的统计资料，
    x23456
    y2.23.85.56.57.0
    由上表可得线性回归方程$\widehaty=\widehatbx+0.08$，若规定当维修费用y＞12时该设各必须报废，据此模型预报该设各使用年限的最大值为（　　）
    A．7B．8C．9D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

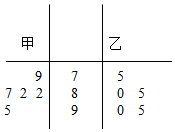    4．甲、乙两位学生参加某项竞赛培训，在培训期间，他们参加的5项预赛成绩的茎叶图记录如下：
    （Ⅰ）从甲、乙两人的成绩中各随机抽取一个，求甲的成绩比乙高的概率；
    （Ⅱ）现要从中选派一人参加该项竞赛，从统计学的角度考虑，你认为选派哪位学生参加合适？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．设数列{an}的前n项和为${S_n}，{a_1}=1，{S_n}=n{a_n}-3n（{n-1}），（{n∈{N^*}}）$．
    （I）求数列{an}的通项公式an；
    （Ⅱ）是否存在正整数n，使得$\frac{S_1}{1}+\frac{S_2}{2}+\frac{S_3}{3}+…+\frac{S_n}{n}-\frac{3}{2}{（{n-1}）^2}=2016$？若存在，求出n值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在等比数列{an}中，a2•a6=3a4，a1=1．数列{bn}是等差数列，b1=a1，b7=a4，则b4=（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设x，y∈R，则“x＞y＞0”是“$\frac{x}{y}$＞1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案