考点:直线与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)连接AC,AC∩BD=O,连接OC
1,则O是AC的中点,利用三角形的中位线的性质证明AC
1∥OP,即可证明AC
1∥平面PBD;
(2)依题意可得PB=
,A
1P=
,A
1B=
,满足A
1P
2+PB
2=A
1B
2,可得A
1P⊥PB,进而可得A
1P⊥PD,由线面垂直的判定定理可得结论;
(3)所求几何体的体积等于四棱柱的体积减去四个体积相等的三棱锥的体积,由数据分别求得体积作差可得答案.
解答:
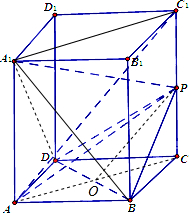
(1)证明:连接AC,AC∩BD=O,连接OC
1,则O是AC的中点,
∵点P是侧棱C
1C的中点,
∴AC
1∥OP,
∵AC
1?平面PBD,OP?平面PBD,
∴AC
1∥平面PBD;
(2)证明:CP=1,CB=1,在Rt△BCP中,PB=
,
同理可知,A
1P=
,A
1B=
所以A
1P
2+PB
2=A
1B
2,则A
1P⊥PB,
同理可证,A
1P⊥PD,
由于PB∩PD=P,PB?平面PBD,PD?平面PBD,
∴A
1P⊥平面PBD.
(3)解:易知三棱锥A
1-BDC
1的体积等于四棱柱的体积减去四个体积相等的三棱锥的体积,
即AB×AD×A
1A-4×
×(
AB×AD)×A
1A=
×1×1×2=
.
点评:本题考查直线与平面、平行垂直的判定,涉及三棱锥体积的求解,属中档题.

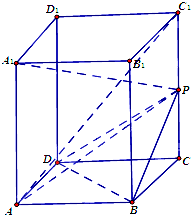 如图,在直四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱C1C垂直于底面ABCD,且C1C=2,点P是侧棱C1C的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,已知底面ABCD是边长为1的正方形,侧棱C1C垂直于底面ABCD,且C1C=2,点P是侧棱C1C的中点. (1)证明:连接AC,AC∩BD=O,连接OC1,则O是AC的中点,
(1)证明:连接AC,AC∩BD=O,连接OC1,则O是AC的中点,

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 已知函数f(x)=2cos(2x+
已知函数f(x)=2cos(2x+