
| A. | sin156°<0 | B. | $cos\frac{16π}{5}>0$ | C. | $tan({-\frac{17π}{8}})<0$ | D. | tan556°<0 |
分析 根据角所在的象限、诱导公式、三角函数值的符号逐项判断即可.
解答 解:A、因为156°在第二象限,所以sin156°>0,故A错误;
B、因为$cos\frac{16π}{5}=cos(3π+\frac{π}{5})$=$-cos\frac{π}{5}<0$,所以B错误;
C、因为$tan(-\frac{17π}{8})=tan(-2π-\frac{π}{8})$=$tan(-\frac{π}{8})<0$,所以C正确;
D、因为tan556°=tan(360°+196°)=tan196°,且196°在第三象限,
所以tan556°>0,故D错误;
故选:C.
点评 本题考查了三角函数的诱导公式,及三角函数在各象限的符号的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
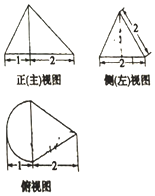
| A. | $\frac{{(4+π)\sqrt{3}}}{3}$ | B. | $\frac{(4+π)\sqrt{3}}{2}$ | C. | $\frac{(4+π)\sqrt{3}}{6}$ | D. | (4+π)$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=30,b=40,A=30° | B. | a=25,b=30,A=150° | ||
| C. | a=8,b=16,A=30° | D. | a=72,b=60,A=135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com