
| A. | a=30,b=40,A=30° | B. | a=25,b=30,A=150° | ||
| C. | a=8,b=16,A=30° | D. | a=72,b=60,A=135° |
分析 由正弦定理可得sinB=$\frac{bsinA}{a}$,根据条件求得sinB的值,根据b与a的大小判断角B的大小,从而判断△ABC的解的个数.
解答 解:对于A:∵a=30,b=40,A=30°,有$\frac{30}{\frac{1}{2}}$=$\frac{40}{sinB}$,
∴sinB=$\frac{2}{3}$,又b>a,故B>A,故B可以是锐角,也可以是钝角,故△ABC有两个解.
对于B:∵b>a,∴B>A=150°,错误,这样的三角形不存在.
对于C:sinB=$\frac{bsinA}{a}$=$\frac{16×\frac{1}{2}}{8}$=1,B为直角,故△ABC有唯一解,
对于D:∵a=72,b=60,A=135°,
由正弦定理得:sinB=$\frac{bsinA}{a}$=$\frac{60×\frac{\sqrt{2}}{2}}{72}$=$\frac{5\sqrt{2}}{12}$,
又b<a,故B<A,故B为锐角,故△ABC有唯一解.
故选:A.
点评 此题属于解三角形的题型,涉及的知识有:正弦定理,三角形的边角关系,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{1}{x}$ | B. | y=sinx+$\frac{1}{sinx}$,x∈(0,$\frac{π}{2}$) | ||
| C. | y=4x+2x,x∈[0,+∞) | D. | y=$\frac{{x}^{2}+3}{\sqrt{{x}^{2}+2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
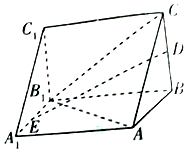 在如图所示的三棱锥ABC-A1B1C1中,AA1⊥底面ABC,D,E分别是BC,A1B1的中点.
在如图所示的三棱锥ABC-A1B1C1中,AA1⊥底面ABC,D,E分别是BC,A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin156°<0 | B. | $cos\frac{16π}{5}>0$ | C. | $tan({-\frac{17π}{8}})<0$ | D. | tan556°<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率( )
在如图所示的正方形中随机掷一粒豆子,豆子落在该正方形内切圆的四分之一圆(如图阴影部分)中的概率( )| A. | $\frac{π}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{π}{16}$ | D. | $\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4\sqrt{6}}{5}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,2] | B. | (-1,+∞) | C. | (-$\frac{1}{2}$,0)∪(0,2) | D. | (-$\frac{1}{2}$,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com