
| ∧ |
| y |
| 7 |
| 26 |
| 推销员编号 | 1 | 2 | 3 |
| 工作年限x(年) | 3 | 5 | 10 |
| 年推销金额y(万元) | 2 | 3 | 4 |
. |
| x |
| 3+5+10 |
| 3 |
. |
| y |
| 2+3+4 |
| 3 |
| 18 |
| 13 |
| ? |
| y |
| 7 |
| 26 |
| 18 |
| 13 |
| ? |
| y |


科目:高中数学 来源: 题型:
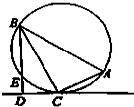 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 4x |
| x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
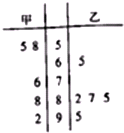 如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为
如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com