
【题目】国际羽毛球比赛规则从2006年5月开始,正式决定实行21分的比赛规则和每球得分制,并且每次得分者发球,所有单项的每局获胜分至少是21分,最高不超过30分,即先到21分的获胜一方赢得该局比赛,如果双方比分为![]() 时,获胜的一方需超过对方2分才算取胜,直至双方比分打成
时,获胜的一方需超过对方2分才算取胜,直至双方比分打成![]() 时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为
时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为![]() ,甲接发球贏球的概率为
,甲接发球贏球的概率为![]() ,则在比分为
,则在比分为![]() ,且甲发球的情况下,甲以
,且甲发球的情况下,甲以![]() 赢下比赛的概率为( )
赢下比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:![]() ,
,![]() ;
;![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)当![]() 时,判断直线
时,判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(Ⅱ)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.
(万亿元)的折线图.

注:年份代码1~9分别对应年份2010~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2019年全国GDP的总量.
的回归方程(系数精确到0.01),预测2019年全国GDP的总量.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,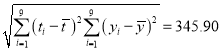 .
.
参考公式:相关系数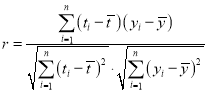 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象的一个对称中心为
的图象的一个对称中心为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A.直线![]() 是函数
是函数![]() 的图象的一条对称轴
的图象的一条对称轴
B.函数![]() 在
在![]() 上单调递减
上单调递减
C.函数![]() 的图象向右平移
的图象向右平移![]() 个单位可得到
个单位可得到![]() 的图象
的图象
D.函数![]() 在
在![]() 上的最小值为
上的最小值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.

(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com