
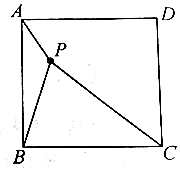
分析 设边长为x(1<x<3)在DABP中,cos$∠ABP=\frac{{x}^{2}+{2}^{2}-{1}^{2}}{4x}$=$\frac{{x}^{2}+3}{4x}$,在DCBP中,cos∠CBP=$\frac{{x}^{2}+{2}^{2}-{3}^{2}}{4x}$=$\frac{{x}^{2}-5}{4x}$,从而($\frac{{x}^{2}+3}{4x}$)2+($\frac{{x}^{2}-5}{4x}$)2=1,由此利用换元法能求出正方形的边长.
解答 解:设边长为x(1<x<3)
在DABP中,cos$∠ABP=\frac{{x}^{2}+{2}^{2}-{1}^{2}}{4x}$=$\frac{{x}^{2}+3}{4x}$,①
在DCBP中,cos∠CBP=$\frac{{x}^{2}+{2}^{2}-{3}^{2}}{4x}$=$\frac{{x}^{2}-5}{4x}$,②
①2+②2得($\frac{{x}^{2}+3}{4x}$)2+($\frac{{x}^{2}-5}{4x}$)2=1,
设x2=t,则1<t<9,得(t+3)2+(t-5)2=16t.
解得${t}_{1}=5+2\sqrt{2}$,${t}_{2}=5-2\sqrt{2}$,
综上所述,正方形的边长为$\sqrt{5+2\sqrt{2}}$,或$\sqrt{5-2\sqrt{2}}$.
点评 本题考查正方形边长的求法,考查余弦定理、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届宁夏高三上月考一数学(文)试卷(解析版) 题型:选择题
下列四个命题:
①命题“若 ,则
,则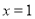 ”的逆否命题为“若
”的逆否命题为“若 ,则
,则 ”;
”;
②“ ”是“
”是“ ”的充分不必要条件;
”的充分不必要条件;
③若 是假命题,则
是假命题,则 均为假命题;
均为假命题;
④对于命题 ,使得
,使得 ,则
,则 为:
为: ,均有
,均有
其中,错误的命题的个数是( )
A.1个 B.2个
C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -35°+k•360°,k∈Z | B. | -325°+k•360°,k∈Z | ||
| C. | 325°+k•360°,k∈Z | D. | 35°+(2k+1)×180°,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com