练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．边界在直线y=0，x=e，y=x及曲线y=$\frac{1}{x}$上的封闭的图形的面积为（　　）
    A．$\frac{3}{2}$B．2C．1D．e

    分析 首先由题意画出图形，明确围成的封闭图形用定积分表示，然后求定积分．

    解答 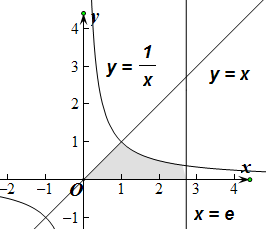解：由题意，直线直线y=0，x=e，y=x及曲线$y=\frac{1}{x}$上所围成的封闭的图形如图：
    直线y=x与曲线y=$\frac{1}{x}$的交点为（1，1），
    所以阴影部分的面积为${∫}_{0}^{1}$xdx+${∫}_{1}^{e}$$\frac{1}{x}$dx=$\frac{1}{2}$x2|${\;}_{0}^{1}$+lnx|${\;}_{1}^{e}$=$\frac{1}{2}$+1=$\frac{3}{2}$，
    故选：A．

    点评 本题考查了利用定积分求曲边梯形的面积；关键是明确被积函数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．设正三棱锥A-BCD的所有顶点都在球O的球面上，BC=1，E，F分别是AB，BC的中点，EF⊥DE，则球O的半径为$\frac{{\sqrt{6}}}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料：
    日期1月10日2月10日3月10日4月10日5月10日6月10日
    昼夜温差x（℃）1011131286
    就诊人数y（人）222529261612
    该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验．
    （1）求选取的2组数据恰好是相邻两个月的概率；
    （2）若选取的是1月与6月的两组数据，请根据2至5月份的数据，求出y关于x的线性回归方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．某产品分甲、乙、丙三级，其中乙、丙两级均属次品，若生产中出现乙级品的概率为0.03，丙级品的概率为0.02，则抽查一件产品是正品的概率为0.95．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若函数f（x）=2sin（ωx-$\frac{π}{3}$）（0＜ω＜π），且f（2+x）=f（2-x），则ω的值为$\frac{5π}{12}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．圆的半径是6cm，则30°的圆心角与圆弧围成的扇形面积是（　　）
    A．$\frac{π}{2}c{m^2}$B．$\frac{3π}{2}c{m^2}$C．πcm2D．3πcm2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．解方程：$\frac{1}{2x-1}$=$\frac{1}{2}-\frac{3}{4x-2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．若函数f（x）=x3-6bx+2b在（0，1）内有极小值，则实数b的取值范围是（0，$\frac{1}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．设m、n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：
    ①若m⊥α，n∥α，则m⊥n；
    ②若α⊥γ，β⊥γ，α∩β=m，则m⊥γ；
    ③若m∥α，n?α，则m∥n；
    ④若α⊥β，α∩β=n，m⊥n，则m⊥β
    其中正确命题的序号是①②．

    查看答案和解析>>

    同步练习册答案