
分析 逐项分析.①根据一次函数的单调性易得;②根据反比例函数的图象和性质易知其值域应为(0,$\frac{1}{2}$);③可举反例说明;④利用均值不等式可得.
解答 解:①当x≤0时,2x+1≤1,故①正确;
②由反比例函数的图象和性质知,当x>2时,$0<\frac{1}{x}<\frac{1}{2}$,故②错误;
③当函数定义域为[0,2]时,函数值域也为[0,4],故③错误;
④当x<0时,$y=x+\frac{1}{x}=-[(-x)+\frac{1}{-x}]$.因为$(-x)+\frac{1}{-x}≥2\sqrt{(-x)•\frac{1}{-x}}=2$,所以y≤-2,故④正确.
综上可知:②③错误.
故答案为:②③.
点评 本题考查函数的概念和性质.利用函数性质和图象是解题关键.其中命题④的判断是本题易错点.属于中档题.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:选择题
| A. | {y|$\frac{1}{2}$<y<1} | B. | {y|0<y$<\frac{1}{2}$} | C. | ∅ | D. | {y|0<y<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天上午下雨,下午不下雨 | |
| B. | 明天下雨的概率为80% | |
| C. | 明天有的地方下雨,有的地方不下雨 | |
| D. | 明天下雨的时间一共是19.2小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
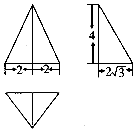
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com