
| A. | 存在x0=$\sqrt{a}$,使得f(x0)<-$\frac{1}{e}$ | B. | 存在x0=$\sqrt{a}$,使得f(x0)>-e | ||
| C. | a的最大值为e3 | D. | 0<a<e3 |
分析 求函数的导数,根据函数存在极小值等价为f′(x)=0有解,转化为一元二次方程,根据一元二次方程根与判别式△之间的关系进行转化求解即可.
解答 解:函数的定义域为(0,+∞),
则函数的导数f′(x)=x-b+$\frac{a}{x}$,
若函数f(x)存在极大值点x0,
则f′(x)=0有解,
即x2-bx+a=0有两个不等的正根,
则 $\left\{\begin{array}{l}{△{=b}^{2}-4a>0}\\{{x}_{1}{+x}_{2}=b>0}\\{{x}_{1}{•x}_{1}=a>0}\end{array}\right.$,得b>2$\sqrt{a}$,(a>0),
由f′(x)=0得x1=$\frac{b-\sqrt{{b}^{2}-4a}}{2}$,x2=$\frac{b+\sqrt{{b}^{2}-4a}}{2}$,
分析易得f(x)的极大值点为x1=x0,
∵b>2$\sqrt{a}$,(a>0),
∴x1=x0=$\frac{b-\sqrt{{b}^{2}-4a}}{2}$=$\frac{2a}{b+\sqrt{{b}^{2}-4a}}$∈(0,$\sqrt{a}$),
则f(x)极大值=f(x0)=x02-bx0+alnx0=$\frac{1}{2}$x02-x02-a+alnx0=-$\frac{1}{2}$x02+alnx0-a,
设g(x)=alnx-$\frac{1}{2}$x2-a,x∈(0,$\sqrt{a}$),
f(x)的极大值恒小于0等价为g(x)恒小于0,
∵g′(x)=$\frac{a}{x}$-x=$\frac{a{-x}^{2}}{x}$>0,
∴g(x)在(0,$\sqrt{a}$)上单调递增,
故g(x)<g($\sqrt{a}$)=aln$\sqrt{a}$-$\frac{3}{2}$a≤0,
得ln$\sqrt{a}$≤$\frac{3}{2}$,即a≤e3,
故a的最大值为是e3,
故选:C.
点评 本题主要考查函数极值的应用,求函数的导数,利用函数极值和导数之间的关系转化为一元二次方程根的与判别式△之间的关系是解决本题的关键.综合性较强,难度大.


科目:高中数学 来源: 题型:选择题
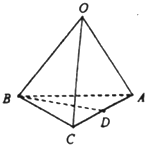 如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )
如图,在三棱锥O-ABC中,点D是棱AC的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{BD}$等于( )| A. | -$\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$ | B. | $\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com