Question

13．已知函数f（x）=$\left\{\begin{array}{l}{（2x-{x}^{2}）{e}^{x}，x≤0}\\{-{x}^{2}+4x+3，x＞0}\end{array}\right.$，g（x）=f（x）-3k，若函数g（x）恰有两个不同的零点，则实数k的取值范围为（1，$\frac{7}{3}$）∪{0，$-\frac{2\sqrt{2}+2}{3{e}^{\sqrt{2}}}$}．

Answer 1

分析 由g（x）=0，利用方程和函数之间的关系，转化为求函数f（x）的极值问题，利用数形结合即可得到结论．

解答 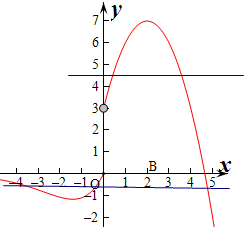解：由g（x）=f（x）-3k=0，即f（x）=3k，
当x≤0时，f（x）=（2x-x²）e^x，
则f'（x）=（2-x²）e^x，由f'（x）=（2-x²）e^x=0，解得x=-$\sqrt{2}$，
当x=-$\sqrt{2}$时，函数f（x）取得极小值f（-$\sqrt{2}$）=$（-2\sqrt{2}-2{）e}^{-\sqrt{2}}$，
当x＞0时，f（x）=-x²+4x+3=-（x-2）²+7≤7，
作出函数f（x）的图象，由图象可知，要使f（x）=3k有恰有两个不同的交点，
则满足3＜3k＜7或$（-2\sqrt{2}-2{）e}^{-\sqrt{2}}$=3k或k=0，
即1＜k＜$\frac{7}{3}$或k=$-\frac{2\sqrt{2}+2}{3{e}^{\sqrt{2}}}$或k=0，
故答案为：（1，$\frac{7}{3}$）∪{0，$-\frac{2\sqrt{2}+2}{3{e}^{\sqrt{2}}}$}

点评 本题主要考查函数零点个数的判定，将方程转化为两个函数的相交个数问题是解决本题问题的基本方法．利用导数研究函数f（x）的极值是解决本题的关键．